前言
最近重新读了BMNet这篇论文,细扒一下论文的细节,同时将细节部分和代码进行一下对应。我对论文关键部分进行了注释,并且注释了数据在网络中的形状变化,方便更好的理解数据是如何被处理的。
论文地址:[2203.08354] Represent, Compare, and Learn: A Similarity-Aware Framework for Class-Agnostic Counting
注释过代码地址:[PaperRecurrent/BMNet–Represent, Compare, and Learn A Similarity-Aware Framework for Class-Agnostic Counting at main · LengNian/PaperRecurrent](https://github.com/LengNian/PaperRecurrent/tree/main/BMNet--Represent%2C Compare%2C and Learn A Similarity-Aware Framework for Class-Agnostic Counting)
整体结构
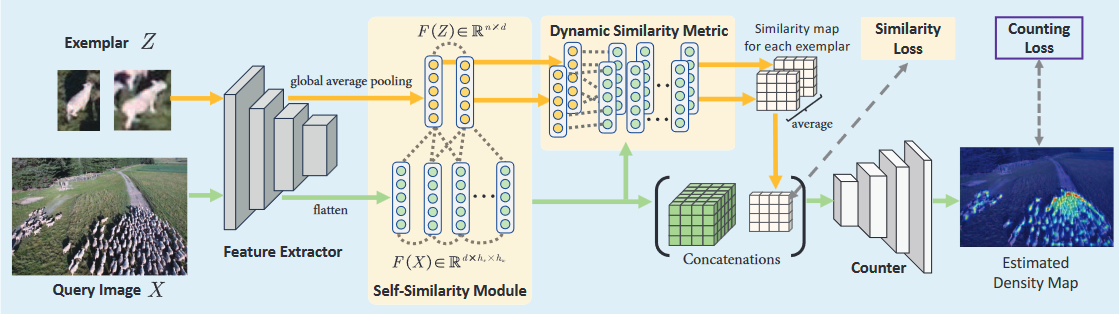
Feature Extractor
对于查询图像X,将其作为输入,经过由卷积层组成的feature extractor,会将其映射为通道数为d的特征,即通过下采样得到$F(x)\in R^{d \times \ h_x \times w_x}$,而对于exemplar Z,会通过全局平均池化得到一个特征向量$F(Z) \in R^d$。
Learning Bilinear Similarity Metric
先前的方法通过固定的内积来计算两个特征向量之间的相似性,作者认为这种方法不能充分的模拟无类别之间的相似性。所以作者将最初的内积扩展到了一种可学习的双线性相似性。
抛开论文不谈,我们需要先知道一下什么是双线性度量。双线性度量是一种用于计算两个特征向量之间相似度或相关性的方法,其思想就是通过一个可学习的权重矩阵W,将两个特征向量x和y映射到一个标量值,用于表示他们的相似度或相关性。
$ Similarity(x, y) = x^T W y $
这里的x和y就是两个输入特征向量,而W是一个可学习的权重矩阵,用于捕获x和y之间的交互关系。
我们再回到论文中,上面可以看到查询图像$F(x) \in R^{d \times h_x \times w_x}$,这里把$F_{ij}(X) \in R^d$ 取出来,$F_{ij}$ 其实就是一个$h_x \times w_x$的特征图。把(i, j)看作是特征图的空间位置。同时定义$x_{ij} = F_{ij}(x)$和$z=F(Z)$。那么双线性度量就可以表示为$x_{ij}^TWz$。论文中又提到提出一种可学曦的双线性度量,所以将W分解并添加偏置,就得到了论文中的公式,即:$S_{ij}(x,z) = (Px_{ij}+b_x)^T (Qz+b_z)$,S是相似图,P和Q就是可学习的指标,b就是偏置,并且$P,Q \in R^{d \times d},b_x,b_z \in R^{d \times 1}$(将W分解为P,Q并且P,Q分别i与query和exemplar对应)。对于n个exemplars,我们可以得到n个相似图,最后对这些相似图进行平均,得到最后的相似图S。
Counter
把特征图F(X)和相似图S堆叠起来我们就得到了Counter的输入,Counter会预测出密度图$D_{pr}$。Counter是由卷积层和双线性上采样层组成。
Learning Dynamic Similarity Metric
在上面我们提到的双线性度量在训练后就固定不变,无法根据样本的特定模式动态调整的,所以作者提出一种动态相似度度量,通过特征选择模块生成针对特定样本的度量。通过SENet的思想,将$Qz+b_z$作为条件,学习一种动态通道权重a,更新后的计算公式即:
$S_{ij}(x,z) = [(Px_{ij}+b_x)]^T [a \circ (Qz+b_z)],\circ$表示哈达玛积,也就是逐元素相乘。
下面这段黑体不需要看之前去看Supervising the Similarity Map这一小节,是我自己没看完代码当时的困惑,而且自己看的过程忽略了相似图的计算并不是在自注意力部分,而是在matcher部分,因为这也是自己的思考,所以就不删除了。
(但这里我有一个不明白的地方,如果将P,Q以及b看作是Linear中学习的参数,作者公式中写的是分别对query的特征图向量和exemplar投影后的向量进行运算,然后对exemplar的运算结果加权,但是代码实现过程中,是将特征图向量和exemplar向量堆叠在一起,再分别利用Linear的参数和偏置进行运算,我认为代码中表达出来的计算公式应该为$S_{ij}(x,z) = [(PU+b_x)]^T [a \circ (QU+b_z)],U=concat[x_{ij}, z] $。,忽略掉)
Supervising the Similarity Map
大部分方法在训练过程中都只使用计数损失进行监督,而直接监督相似性匹配可以使相似性更好的建模,所以作者提出一种监督方式可以指导相似度的建模。假设相似图的尺寸是queryd的1/r,那么S中的一个点就代表query中的r * r个点。对于S中的每一个点如果他所包含query中的r * r个点中包含了超过一个或多个的目标,那么就给他指派一个正标签,否则就是负标签,我们就得到了相似性度量损失。
$ L_{sim} = -log \frac{\sum_{i \in pos}exp(S_i)}{\sum_{i \in pos}exp(S_i) + \sum_{j \in neg}exp(S_j)} $,通过这个公式,我们将最大化正标签在所有标签中的比例。
Self-Similarity Module
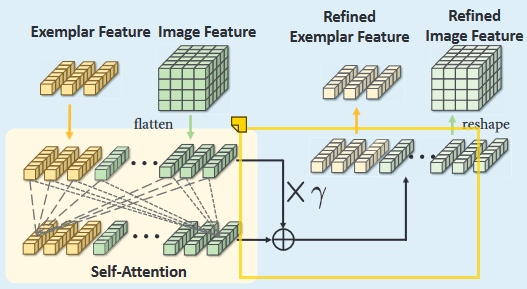
同一类别外形等各方面也会有各种不同的变化等,比如姿势,比例,这又给相似度匹配带来挑战,所以作者提出自注意力模块解决该问题。从query中提取每个特征向量$F_{ij}(x)$,将示例特征F(Z)和其收集到一个特征集合中,然后进行自注意力,自注意力之后的结果会与原始特征进行加权融合即$F_{final} = F_{original} + \gamma F_{update} $。然后将加权融合以后的特征再重新变为exemplar和query,并且这里的$\gamma $也是一个可学习的参数。
这里作者说是将收集特征图向量(也就是$F_{ij}X \in R^{d} $) 和exemplar特征组成一个特征集,实际在代码中就是通过堆叠query的特征图和exemplar映射成的特征向量,然后通过矩阵乘法达到每个向量之间计算相似度的目的
scale embed
对图像大小的调整和特征提取过程中的池化操作损失了scale信息。所以作者提出了使用对应的scale embedding去弥补这部分丢失的信息。
我的理解是将尺度空间离散化为多个等级$l_{total}$,不同等级对应着一个d维的嵌入向量,那么总共就会有$l_{total}$个嵌入向量。
对于Query X和exemplar Z,会计算exemplar的尺度等级l(Z),$ l(Z) = min(l_{total}-1, \lfloor(\frac{h_Z}{2h_X}+\frac{w_Z}{2w_Z} \cdot ) \cdot l_{total} \rfloor )$,得到尺度等级l(Z)以后,就可以选择对应的d维嵌入向量添加到exemplar中以增强其特征表示。
实验细节
限制query的大小,将其限制在[384, 1584]以内,exemplar的大小调整为128 * 128。
特征提取器的输出通道为1024,对于query,使用1 * 1卷积将其通道减小为256,对于exemplar使用全局平均池化和线性层得到一个256维的张量。
Counter包含了一系列双线性上采样层和卷积层,最后的密度图和输入图像的大小是保持一致的。
