前言
初次接触对抗样本，在这里记录一下自己的学习过程，希望可以帮助自己更好理解，也希望可以帮助到有需要的人。
FGSM
FGSM原理
FGSM，即Fast Gradient Sign Method，这是一种用于生成对抗性样本的算法。在论文Explaining and Harnessing Adversarial Examples中被提到。它是一种基于梯度生成的算法，属于无目标攻击（不要求指定生成的对抗样本的类别，只要求生成的对抗样本不是正确的那个类别即可）
在这幅图最左侧是输入图像x，他的正确分类标签y为”panda”，我们将中间这幅图所表达的意思用μ来代替，即μ=0.07*(sign(J(θ,x,y)‘))，其中sign是符号函数，J(θ,x,y)是训练网络的损失函数，J(θ,x,y)’表示损失函数J对x的导数。用x’代表生成的对抗样本，即x‘=x+μ。从图中可以看到x’的分类标签y’成为了”gibbon“。说明对抗样本成功骗过了模型，使模型的分类错误。
在神经网络中使用梯度下降算法，使梯度降低，从而不断最小化损失值以达到提高准确率的目的。其公式如下：
$$
\alpha = \alpha - \delta\times\frac{\partial L}{\partial \alpha} \tag{1}
$$
如果把梯度下降中的后一项看成μ，即
$$
\eta = \delta\times\frac{\partial L}{\partial \alpha} \tag{2}
$$
那么，梯度下降的公式就可以写为:
$$
\alpha = \alpha - \eta \tag{3}
$$
这与FGSM中x'=x+μ的公式非常像，为什么这么像呢？
梯度代表函数值增加最快的方向，在神经网络中我们要通过反向传播不断降低损失值来达到提高准确率的目的，所i有要减去梯度，而在fgsm中，为了让分类错误，要让损失增大也就是梯度上升，所以这里只需要改为加号就可以了。所以这两个公式是非常像的。
我再写一下我对损失增大的理解，我们直到损失函数是度量真实值与预测值之间的差距的，当损失值越小，说明预测值和真实值越接近，而我们这里是要让分类错误，就是预测值和真实值不同，所以要让这个度量指标变大，其越大说明预测值和真实值之间的差距越大，也就说明模型的分类是错误的。
接下来我们介绍一下FGSM算法中的μ，公式如下：
$$
\mu = \epsilon sign(\nabla_xJ(\boldsymbol{\theta},\boldsymbol{x},y)) \tag{4}
$$
在这个公式中，x是输入的原始图像，θ是模型的参数，y是原始图像x的真实类别，J是损失函数，∇x 表示对 x 求偏导，sign是符号函数。我们在这里看一下符号函数的公式。
$$
\text{sign}(x) =
\begin{cases}
-1 & \text{if } x < 0, \\
0 & \text{if } x = 0, \\
1 & \text{if } x > 0.
\end{cases}
\tag{5}
$$
在FGSM中引入符号函数可以确定对抗扰动的方向。在FGSM中不需要关心具体的梯度大小，只需要知道方向即可通过确定对抗扰动的方向。（**这里我的理解是，FGSM要寻找一个可以使模型分类错误的有效扰动，而不是最优的扰动的大小，所以只关心梯度方向，具体扰动大小则由epsilon确定，初次之外，有资料中说，对抗性扰动的泛化性因不同的模型和数据集，具体的梯度大小会有所不同，而梯度方向包含了导致模型判断错误的关键信息，所以更注重梯度的方向。对于使用符号函数的相关原因，欢迎大家一起讨论。**）
这里的ε控制着扰动的大小。ε较小，对抗扰动不易被察觉，如果过大，扰动会很明显，容易被识别出来。
Pytorch代码实现
FGSM的代码在Pytorch已经实现(Adversarial Example Generation — PyTorch Tutorials 2.4.0+cu124 documentation)
def FGSM_attack(image, epsilons, data_grad):
# 符号函数
sign_data_grad = data_grad.sign()
# 实现上述(5)公式
perturbed_image = image + epsilons * sign_data_grad
# 限制元素值在指定的范围内
perturbed_image = torch.clamp(perturbed_image, 0, 1)
return perturbed_image训练+攻击完整代码
这部分自己搭建一个LeNet神经网络，并在MNIST手写数据集上进行训练，之后使用FGSM方法去生成对抗样本，测试训练的网络的分类准确率。
搭建LeNet模型
# 搭建LeNet模型
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
# 卷积层
self.conv = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
# 全连接层
self.fc = nn.Sequential(
nn.Linear(in_features=16 * 5 * 5, out_features=120),
nn.ReLU(),
nn.Linear(in_features=120, out_features=84),
nn.ReLU(),
nn.Linear(in_features=84, out_features=10)
)
def forward(self, img):
img = self.conv(img)
img = img.view(img.size(0), -1)
out = self.fc(img)
return out
net = LeNet()
net = net.to(device)# 使用设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
mean = 0.1307
std = 0.3801
# 对图像变换
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((mean,), (std,))
]
)# 训练数据集, 测试数据集
train_dataset = datasets.MNIST('../datasets/MNIST', train=True, transform=transform, download=True) # len 60000
test_dataset = datasets.MNIST('../datasets/MNIST', train=False, transform=transform, download=True) # len 10000
# 数据迭代器
train_dataloader = DataLoader(train_dataset, batch_size=64, shuffle=True) # len 938
test_dataloader = DataLoader(test_dataset, batch_size=64, shuffle=True) # len 157lr = 1e-3
epochs = 30
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
criterion = nn.CrossEntropyLoss()
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', factor=0.5, verbose=True, patience=5, min_lr=0.0000001)以上都是为训练模型进行准备，下面开始对模型进行训练。
train_loss = []
train_acc = []
val_loss = []
val_acc = []
for epoch in tqdm(range(epochs)):
train_losses = 0
train_acces = 0
val_losses = 0
val_acces = 0
for x, y in train_dataloader:
x, y = x.to(device), y.to(device)
output = net(x)
# 计算loss
loss = criterion(output, y)
# 计算预测值
_, pred = torch.max(output, axis=1)
# 计算acc
acc = torch.sum(y == pred) / output.shape[0]
# 反向传播
# 梯度清零
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_losses += loss.item()
train_acces += acc.item()
train_loss.append(train_losses / len(train_dataloader))
train_acc.append(train_acces / len(train_dataloader))
# 模型评估，这里就使用测试集进行验证了，实际应该再划分验证集
net.eval()
with torch.no_grad():
for x, y in test_dataloader:
x, y = x.to(device), y.to(device)
output = net(x)
loss = criterion(output, y)
scheduler.step(loss)
_, pred = torch.max(output, axis=1)
acc = torch.sum(y == pred) / output.shape[0]
val_losses += loss.item()
val_acces += acc.item()
val_loss.append(val_losses / len(test_dataloader))
val_acc.append(val_acces / len(test_dataloader))
print(f"epoch:{epoch+1} train_loss:{train_losses / len(train_dataloader)}, train_acc:{train_acces / len(train_dataloader)}, val_loss:{val_losses / len(test_dataloader)}, val_acc:{val_acces / len(test_dataloader)}")
plt.plot(train_loss, color='green', label='train loss')
plt.plot(val_loss, color='blue', label='val loss')
plt.legend()
plt.xlabel("epoch")
plt.ylabel("loss")
plt.show()
plt.plot(train_acc, color='green', label='train acc')
plt.plot(val_acc, color='blue', label='val acc')
plt.legend()
plt.xlabel("epoch")
plt.ylabel("acc")
plt.show()
# 保存训练好的模型
PATH = './fgsm_mnist_lenet.pth'
torch.save(net, PATH) 3%|▎ | 1/30 [00:09<04:37, 9.58s/it]
epoch:1 train_loss:0.23495538183736173, train_acc:0.9266890991471215, val_loss:0.06610820889117042, val_acc:0.9808917197452229
7%|▋ | 2/30 [00:18<04:22, 9.37s/it]
epoch:2 train_loss:0.0733803818781755, train_acc:0.9775286513859275, val_loss:0.06484267477741003, val_acc:0.981687898089172
10%|█ | 3/30 [00:27<04:10, 9.26s/it]
epoch:3 train_loss:0.07191201691368797, train_acc:0.9779784115138592, val_loss:0.0649121593102623, val_acc:0.9818869426751592
13%|█▎ | 4/30 [00:36<03:56, 9.08s/it]
epoch:4 train_loss:0.07054272936885433, train_acc:0.9782949093816631, val_loss:0.06256632373674186, val_acc:0.9819864649681529
17%|█▋ | 5/30 [00:45<03:45, 9.00s/it]
epoch:5 train_loss:0.06927903689968307, train_acc:0.9787446695095949, val_loss:0.06133736597943553, val_acc:0.9821855095541401
20%|██ | 6/30 [00:54<03:31, 8.80s/it]
epoch:6 train_loss:0.06818971440974456, train_acc:0.9791611140724946, val_loss:0.06043949323130926, val_acc:0.982484076433121
23%|██▎ | 7/30 [01:03<03:27, 9.01s/it]
epoch:7 train_loss:0.06716231363557422, train_acc:0.9793943230277186, val_loss:0.06052255801631102, val_acc:0.9821855095541401
27%|██▋ | 8/30 [01:12<03:19, 9.06s/it]
epoch:8 train_loss:0.0663046940549541, train_acc:0.9796108742004265, val_loss:0.05889693624933197, val_acc:0.9826831210191083
30%|███ | 9/30 [01:20<03:05, 8.85s/it]
epoch:9 train_loss:0.06548984157693967, train_acc:0.9798773987206824, val_loss:0.05827412447613326, val_acc:0.982484076433121
33%|███▎ | 10/30 [01:30<02:59, 8.97s/it]
epoch:10 train_loss:0.0647883117283339, train_acc:0.9800106609808102, val_loss:0.058015704478261765, val_acc:0.9823845541401274
37%|███▋ | 11/30 [01:38<02:47, 8.83s/it]
epoch:11 train_loss:0.06416832418121429, train_acc:0.9802105543710021, val_loss:0.0571870897817989, val_acc:0.982484076433121
40%|████ | 12/30 [01:47<02:38, 8.82s/it]
epoch:12 train_loss:0.06361952270947095, train_acc:0.980410447761194, val_loss:0.05745712512582066, val_acc:0.9821855095541401
43%|████▎ | 13/30 [01:56<02:30, 8.86s/it]
epoch:13 train_loss:0.06314356109725117, train_acc:0.980577025586354, val_loss:0.056493567623150574, val_acc:0.9826831210191083
47%|████▋ | 14/30 [02:06<02:25, 9.07s/it]
epoch:14 train_loss:0.06276988985686144, train_acc:0.9806603144989339, val_loss:0.05619345570078037, val_acc:0.9825835987261147
50%|█████ | 15/30 [02:15<02:19, 9.28s/it]
epoch:15 train_loss:0.0624012095647167, train_acc:0.9807769189765458, val_loss:0.05572936845836556, val_acc:0.9825835987261147
53%|█████▎ | 16/30 [02:25<02:11, 9.42s/it]
epoch:16 train_loss:0.06199908992553602, train_acc:0.9808268923240938, val_loss:0.055503922487923484, val_acc:0.9827826433121019
57%|█████▋ | 17/30 [02:35<02:04, 9.58s/it]
epoch:17 train_loss:0.06172961615838174, train_acc:0.9809101812366737, val_loss:0.05556283311052307, val_acc:0.9825835987261147
60%|██████ | 18/30 [02:45<01:57, 9.77s/it]
epoch:18 train_loss:0.06138933949651065, train_acc:0.9810934168443497, val_loss:0.054954844592198446, val_acc:0.982484076433121
63%|██████▎ | 19/30 [02:54<01:43, 9.43s/it]
epoch:19 train_loss:0.06114780887026094, train_acc:0.9812599946695096, val_loss:0.054730413220585535, val_acc:0.982484076433121
67%|██████▋ | 20/30 [03:03<01:33, 9.36s/it]
epoch:20 train_loss:0.060946285610458555, train_acc:0.9813266257995735, val_loss:0.0545463676187714, val_acc:0.982484076433121
70%|███████ | 21/30 [03:13<01:25, 9.45s/it]
epoch:21 train_loss:0.06072342605652736, train_acc:0.9813266257995735, val_loss:0.05441298720776845, val_acc:0.9826831210191083
73%|███████▎ | 22/30 [03:22<01:15, 9.47s/it]
epoch:22 train_loss:0.060515265972383304, train_acc:0.9814598880597015, val_loss:0.054409430030092694, val_acc:0.9827826433121019
77%|███████▋ | 23/30 [03:31<01:04, 9.28s/it]
epoch:23 train_loss:0.060337386706641426, train_acc:0.9815265191897654, val_loss:0.05422507992287161, val_acc:0.9827826433121019
80%|████████ | 24/30 [03:39<00:53, 8.98s/it]
epoch:24 train_loss:0.0602028726938683, train_acc:0.9815931503198294, val_loss:0.055592933979632844, val_acc:0.9822850318471338
83%|████████▎ | 25/30 [03:48<00:44, 8.93s/it]
epoch:25 train_loss:0.06003174935030674, train_acc:0.9816098081023454, val_loss:0.05382291597438751, val_acc:0.9830812101910829
87%|████████▋ | 26/30 [03:58<00:36, 9.08s/it]
epoch:26 train_loss:0.05991259947724974, train_acc:0.9816597814498934, val_loss:0.05371515328586576, val_acc:0.9831807324840764
90%|█████████ | 27/30 [04:06<00:26, 8.91s/it]
epoch:27 train_loss:0.059782677139443505, train_acc:0.9816930970149254, val_loss:0.05411682381727703, val_acc:0.9826831210191083
93%|█████████▎| 28/30 [04:16<00:18, 9.08s/it]
epoch:28 train_loss:0.05965107033448194, train_acc:0.9817097547974414, val_loss:0.053595036425432015, val_acc:0.9829816878980892
97%|█████████▋| 29/30 [04:25<00:09, 9.30s/it]
epoch:29 train_loss:0.059546736687092164, train_acc:0.9816930970149254, val_loss:0.0533999552309608, val_acc:0.9830812101910829
100%|██████████| 30/30 [04:35<00:00, 9.19s/it]
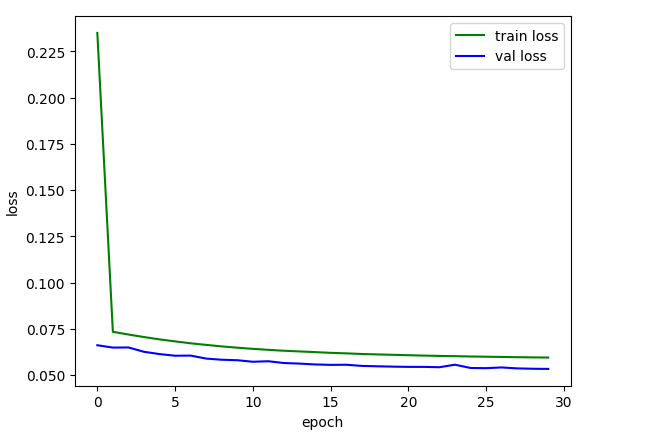
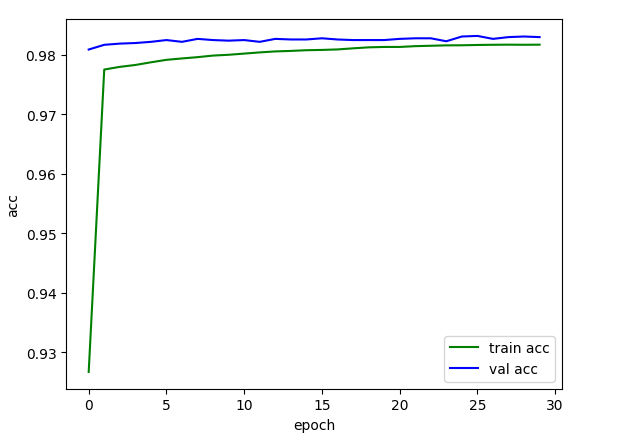
epoch:30 train_loss:0.05946045447769426, train_acc:0.9817097547974414, val_loss:0.053309381550925364, val_acc:0.9829816878980892经过30轮的训练，模型的再训练集和验证集上的准确率大概达到了98%。
因为训练轮数很少，所以这条曲线看起来并不平滑，但基本收敛，实际应用时，可以将训练轮数增加。
如果已经有训练好的模型，可以使用以下代码进行加载：
# 自己根据实际情况修改模型存储路径
PATH = './fgsm_mnist_lenet.pth'
net = torch.load(PATH)
net = net.to(device)为了方便之后的操作，这里修改一下batch_size的大小，修改为1。
test_dataloader = DataLoader(test_dataset, batch_size=1, shuffle=True) 对对抗样本测试的函数
# 测试函数 FGSM
def test_FGSM(model, device, test_dataloader, epsilons):
correct = 0
adv_examples = []
for data, target in test_dataloader:
data, target = data.to(device), target.to(device)
# 设置张量的属性，对于攻击十分关键
data.requires_grad = True
# 前向传播
output = model(data)
_, init_pred = torch.max(output, axis=1)
# init_pred = output.max(1, keepdim=True)[1]
# print(init_pred)
# print(target)
# 如果分类错误就不去扰动图像
if init_pred.item() != target.item():
# print("Original image's predict is wrong!")
# print("init_pred:", init_pred)
# print("true_pred:", target)
continue
# 负对数似然损失
loss = F.nll_loss(output, target)
model.zero_grad()
loss.backward()
# 收集数据损失
# data.grad 是一个完整的梯度张量，可以用于进一步的梯度计算，
# 而 data.grad.data 是梯度张量的数据内容，通常用于查看或操作梯度的具体数值，但不用于梯度计算。
data_grad = data.grad.data
# 使用FGSM进行攻击
perturbed_data = FGSM_attack(data, epsilons, data_grad)
# 对扰动后的图像进行重新分类
output = model(perturbed_data)
_, attack_pred = torch.max(output, axis=1)
# 模型对对抗样本的分类还是正确的
if attack_pred.item() == target.item():
correct += 1
# 保存噪声为0的5个图像用于后期的可视化
if(epsilons == 0) and (len(adv_examples) < 5):
adv_ex= perturbed_data.squeeze().detach().cpu().numpy()
# 保留正确标签, 攻击后标签, 攻击后图像
adv_examples.append((init_pred.item(), attack_pred.item(), adv_ex))
# 保留5个攻击后分类错误的实例
else:
if len(adv_examples) < 5:
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
# 同样保存正确标签，攻击后标签，攻击后图像
adv_examples.append((init_pred.item(), attack_pred.item(), adv_ex))
# 被攻击后的分类准确率
attack_acc = correct / len(test_dataloader)
print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilons, correct, len(test_dataloader), attack_acc))
# 返回当前保存的攻击样本的相关内容和测试准确率
return adv_examples, attack_acc接下来就是使用不同的eplison值生成对抗样本，并使用上述的测试函数进行测试。
accuracies = []
examples = []
# eps=0表示未受到攻击的测试准确性
epsilons = [0, .2, .4, .5, .6, .65, .7]
for eps in epsilons:
ex, acc = test_FGSM(net, device, test_dataloader, eps)
accuracies.append(acc)
examples.append(ex)
可视化不同epsilon下的准确率
plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.title("Accuracy vs Epsilon -- FGSM")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()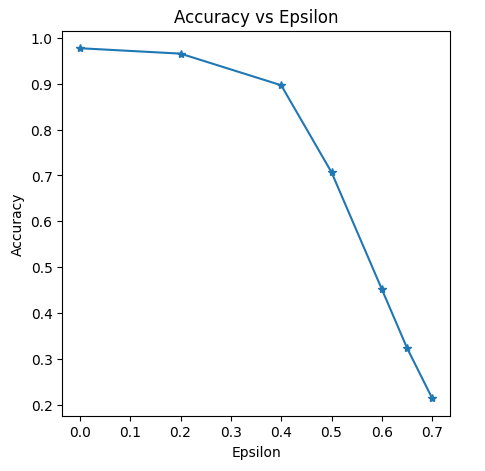
可视化保存的不同epsilon下生成的对抗样本。
index = 0
plt.figure(figsize=(8, 10))
for i in range(len(epsilons)):
for j in range(len(examples[i])):
index += 1
plt.subplot(len(epsilons), len(examples[i]), index)
if j == 0:
plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
init_pred, attack_pred, example = examples[i][j]
plt.title("{} --> {}".format(init_pred, attack_pred))
plt.imshow(example)
plt.tight_layout()
# plt.show()
当epsilon为0时，其实就是没有做什么扰动，可以看到，随着epsilon值的提高，图像的扰动也是可以被察觉到的，值越大，扰动越明显。
参考文献
2.基于梯度的攻击——FGSM - 机器学习安全小白 - 博客园 (cnblogs.com)（这篇文章中有作者对使用符号函数确定方向的思考）
对抗攻击(一) FGSM - HickeyZhang - 博客园 (cnblogs.com)（这篇文章对FGSM中要让损失函数增加的数学解释）
对抗样本之FGSM原理&coding_fgsm是有目标还是无目标的-CSDN博客
GAN 系列的探索与pytorch实现 (数字对抗样本生成)_pytorch课程设计-CSDN博客（由于我的能力有限，所以本文的代码主要参考参考文献中的后两篇文章）
BIM(I-FGSM)
I-FGSM原理
在FGSM算法中，生成的对抗样本是通过x‘=x+μ进行单步攻击，直接在原图像中加上扰动得到的，其中μ=ϵ∗sign(∇xJ(x,y))，也就是说是将每个像素点都变化了ε这么多。而I-FGSM算法是使用迭代的方法，寻找各个像素点的扰动，在FGSM的基础上进行了多次迭代。
迭代的作用就是使新样本在旧样本的基础上每个像素点变化α，然后通过裁剪，控制得到的新样本各像素都在原始图像的ε领域内。这句话通过公式可以很好理解：
$$
\boldsymbol{X_0^{adv}} = \boldsymbol{X}, \quad \boldsymbol{X_{N+1}^{adv}}=Clip_{\boldsymbol{X}, \epsilon}\{\boldsymbol{X_{N}^{adv}} + \alpha sign(\nabla_XJ(\boldsymbol{X_{N}^{adv}, y_{true}})) \} \tag{1}
$$
Pytorch代码实现
在许多文章中，我看到对于BIM算法的实现就是简单简单的循环了FGSM算法(这样做我认为是不对的，因为忽视了ε和α参数的使用)，但是从公式中我们是可以看到，需要用α控制移动步长和ε来控制像素的变化范围，所以结合自己的理解，我修改了原始FGSM算法，得到以下I-FGSM的核心算法。
def I_FGSM_attack(ori_images, adv_images, epsilon, alpha, data_grad):
sign_data_grad = data_grad.sign()
perturbed_image = adv_images + alpha * sign_data_grad
perturbed_image = torch.clamp(perturbed_image, ori_images - epsilon, ori_images + epsilon)
return perturbed_image相比原始的FGSM算法
def FGSM_attack(image, epsilons, data_grad):
sign_data_grad = data_grad.sign()
perturbed_image = image + epsilons * sign_data_grad
perturbed_image = torch.clamp(perturbed_image, 0, 1)
return perturbed_image首先是传入函数参数的变化，I-FGSM函数需要计算原始图像的ε的范围，所以有参数ori_images和epsilon，然后对每次得到的样本进行扰动，最后将其范围限制在原始图像像素-ε和原始图像+ε。
代码实现
这里就使用上文FGSM中所训练得到的模型，所以训练等代码和前面的一样，直接从测试开始。
# 测试函数 BMI/I-FGSM
def test_I_FGSM(model, device, test_dataloader, epsilons, alpha, iters=40):
correct = 0
adv_examples = []
for data, target in test_dataloader:
data, target = data.to(device), target.to(device)
# 设置张量的属性，对于攻击十分关键
data.requires_grad = True
# 前向传播
output = model(data)
_, init_pred = torch.max(output, axis=1)
# 如果分类错误就不去扰动图像
if init_pred.item() != target.item():
continue
# 保存原始数据，并且不共享，用于在torch.clamp中使用
ori_data = data.detach().clone()
# epsilons == 0时,就是不添加任何扰动进行一次测试,反复迭代就是浪费计算资源
if alpha != 0:
for k in range(iters):
# 负对数似然损失
output = model(data)
loss = F.nll_loss(output, target)
model.zero_grad()
loss.backward()
# 收集数据损失
# data.grad 是一个完整的梯度张量，可以用于进一步的梯度计算，
# 而 data.grad.data 是梯度张量的数据内容，通常用于查看或操作梯度的具体数值，但不用于梯度计算。
data_grad = data.grad.data
# 使用I-FGSM进行攻击, 每次都是在上一次的基础上进行扰动
data = I_FGSM_attack(ori_data, data, epsilons, alpha, data_grad)
# 迭代求对抗样本中，需要及时的使用截断detach将重复使用变量，变成计算图中的叶子节点；
# 由于变成了叶子节点，后续还需要对该变量求偏导，故添加requires_grad参数
# 在I-FGSM中是要计算损失函数对xt的梯度，而data(就是这里的xt)是通过函数计算出来的,
# 他的grad_fn是其对应的类型实际计算中不会计算L对xt的梯度，xt只是一个中间过程
# 这里用detach_()把他变成一个叶子结点,那么就可以计算到L对xt的梯度
data.detach_()
data.requires_grad = True
# 对扰动后的图像进行重新分类
output = model(data)
_, attack_pred = torch.max(output, axis=1)
# 说明攻击后的分类还是正确的
if attack_pred.item() == target.item():
correct += 1
# 保存噪声为0的5个图像用于后期的可视化
if(epsilons == 0) and (len(adv_examples) < 5):
adv_ex= data.squeeze().detach().cpu().numpy()
# 保留正确标签, 攻击后标签, 攻击后图像
adv_examples.append((init_pred.item(), attack_pred.item(), adv_ex))
# 保留攻击后分类错误的实例
else:
if len(adv_examples) < 5:
adv_ex = data.squeeze().detach().cpu().numpy()
adv_examples.append((init_pred.item(), attack_pred.item(), adv_ex))
# 被攻击后的分类准确率
attack_acc = correct / len(test_dataloader)
print("Alpha: {:.4f}\tTest Accuracy = {} / {} = {}".format(alpha, correct, len(test_dataloader), attack_acc))
return adv_examples, attack_acc这里为了方便，我没有调整ε的值，固定ε的值，调整了α，同时为了方便，也需要将测试数据加载器的batch_size设置为1。
accuracies = []
examples = []
epsilons = 0.3
alphas = [0, 2/512, 2/255, 2/128, 2/64, 2/32]
for alpha in alphas:
ex, acc = test_I_FGSM(net, device, test_dataloader, epsilons, alpha)
accuracies.append(acc)
examples.append(ex)# 测试结果
Alpha: 0.0000 Test Accuracy = 9833 / 10000 = 0.9833
Alpha: 0.0039 Test Accuracy = 9378 / 10000 = 0.9378
Alpha: 0.0078 Test Accuracy = 8126 / 10000 = 0.8126
Alpha: 0.0156 Test Accuracy = 3150 / 10000 = 0.315
Alpha: 0.0312 Test Accuracy = 2407 / 10000 = 0.2407
Alpha: 0.0625 Test Accuracy = 2204 / 10000 = 0.2204可视化结果
plt.figure(figsize=(5,5))
plt.plot(alphas, accuracies, "*-")
plt.title("Accuracy vs Alpha -- I-FGSM")
plt.xlabel("Alpha")
plt.ylabel("Accuracy")
plt.show()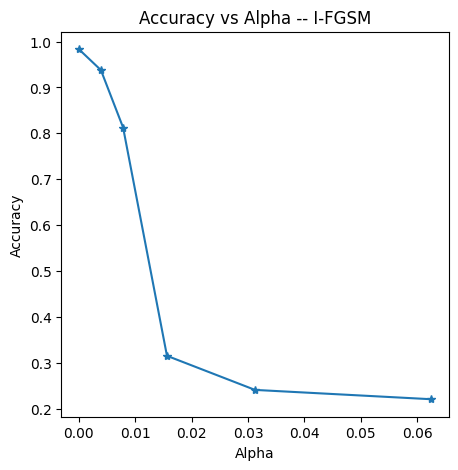
在这个结果中，α从0.0078到0.0156的过程有大量的样本被攻击成功，读者可以试着修改α，ε还有iters等参数去进行修改。
index = 0
plt.figure(figsize=(8, 10))
for i in range(len(alphas)):
for j in range(len(examples[i])):
index += 1
plt.subplot(len(alphas), len(examples[i]), index)
if j == 0:
plt.ylabel("Alpha: {:.4f}".format(alphas[i]), fontsize=14)
init_pred, attack_pred, example = examples[i][j]
plt.title("{} --> {}".format(init_pred, attack_pred))
plt.imshow(example)
plt.tight_layout()
# plt.show()
从可视化的结果中也可以看出，随着alpha的增大，对图像扰动的增加也越来越明显。
参考文献
对抗样本生成方法综述（FGSM、BIM\I-FGSM、PGD、JSMA、C&W、DeepFool）-CSDN博客
