前言
最近我想使用Mamba去代替一下Transformer,所以在b站看了耿直哥老师的讲解视频,前半段所有内容几乎全部来自视频内容。
如果想看我自己总结的部分,可以直接跳转到补充部分
最近自己又看到几篇文章感觉讲的非常好,也在这里一同推荐给大家。
Mamba详解(一)之什么是SSM? - 知乎 这篇文章的一系列感觉都很清晰,可以在作者文章中找到其它部分
一文通透想颠覆Transformer的Mamba:从SSM、HiPPO、S4到Mamba(被誉为Mamba最佳解读)_mamba模型-CSDN博客
参考文献
AI大讲堂:革了Transformer的小命?专业拆解【Mamba模型】_哔哩哔哩_bilibili
A Visual Guide to Mamba and State Space Models - Maarten Grootendorst
一文通透想颠覆Transformer的Mamba:从SSM、HiPPO、S4到Mamba(被誉为Mamba最佳解读)_mamba模型-CSDN博客
关于安装mamba_ssm我主要参考了这几篇文章
Ubuntu和Windows系统之Mamba_ssm安装 - 技术栈
配置mamba-ssm环境的乱七八糟的可能有用的操作 - 知乎
mamba_ssm和causal-conv1d详细安装教程_causal-conv1d离线安装包-CSDN博客
Transformer缺点
位置编码:把时序内容空间化
对于transformer来说,其中的自注意力机制存在一个天然的缺陷,就是其自注意力机制的计算范围仅仅局限在了窗口内,而忽略了窗口外的元素,这就造成了视野狭窄,缺乏了全局观。如果增加窗口的长度,那么计算量会呈平方增长。
本质上说,Transformer就是通过位置编码,将序列数据空间化,然后通过计算空间相关度方向建模时序相关度,这个过程忽视了数据内在结构的关联关系。 (我的理解就是对于输入数据,无论其是否冗余或者是否重要,都统一进行位置编码,然后将其空间化,计算其空间相关度)。但是这种做法是在当年为了充分利用GPU的并行能力,SSM类模型(时序状态空间模型SSM)就是让长序列数据建模回归传统,这是其思考问题的初衷和视角。
时序状态空间模型SSM
连续空间的时序建模
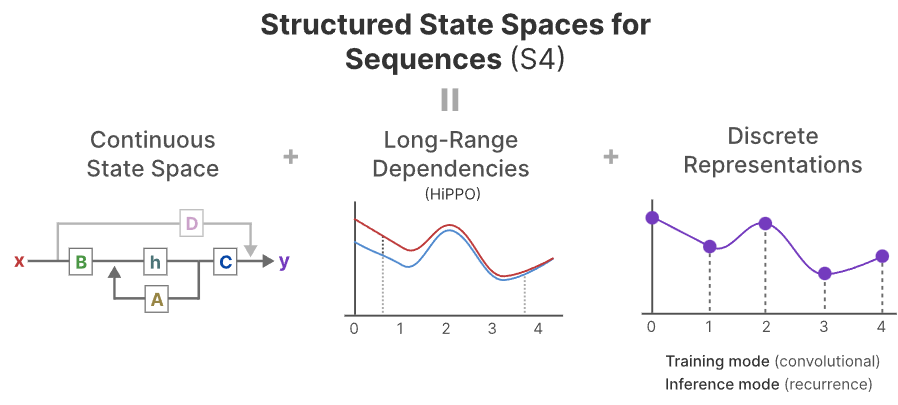
Mamba是基于结构化状态空间序列模型(SSMs),对应论文[2110.13985] Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers
上面这篇论文本质也是RNN模型。
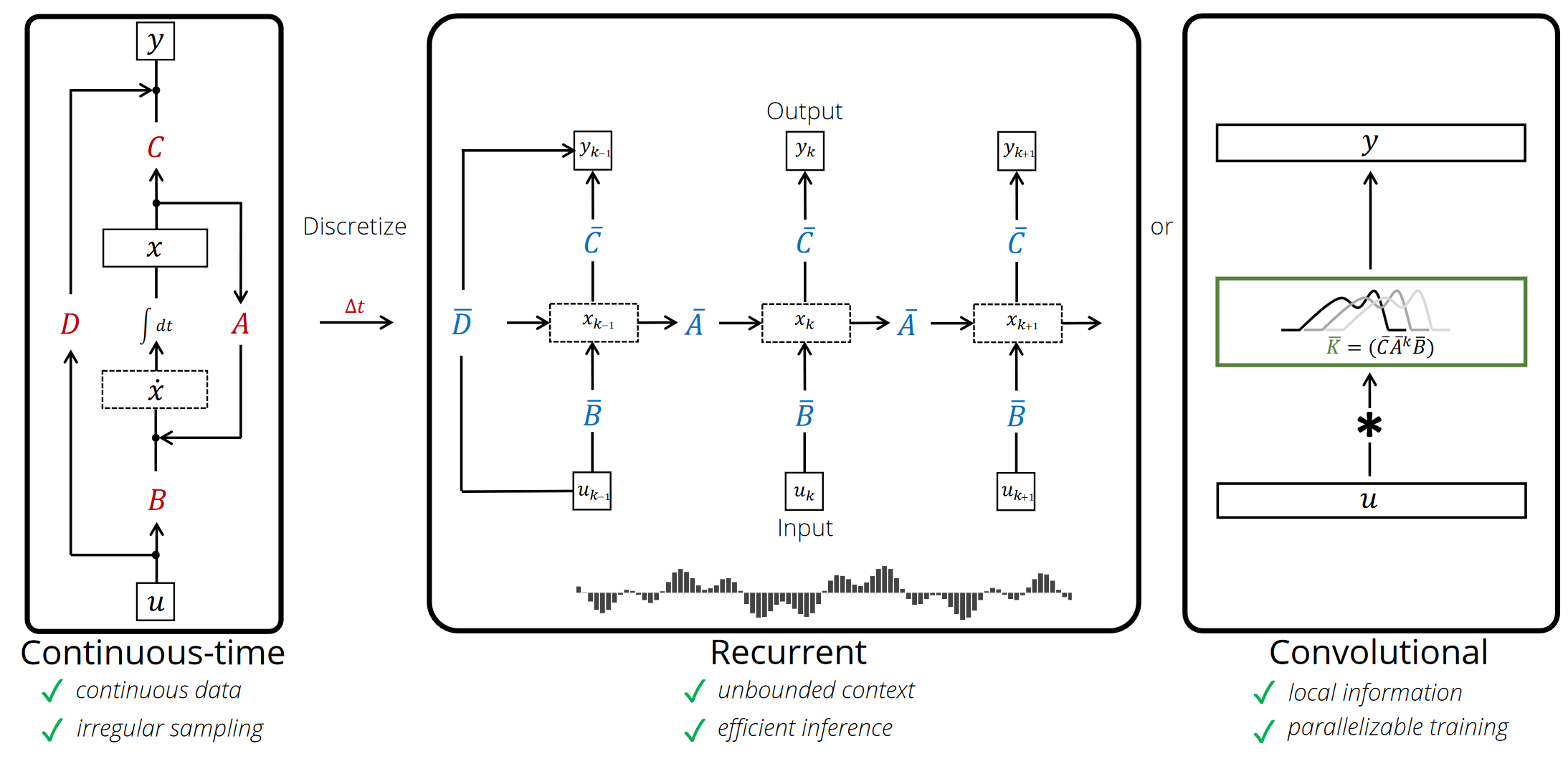
这一段其实就是解释了上图中Continuous-time所对应的内容。绝大部分情况下,都是时变的,是动态的,而非时不变的。
时序离散化与RNN
其对应Recurrent这部分。

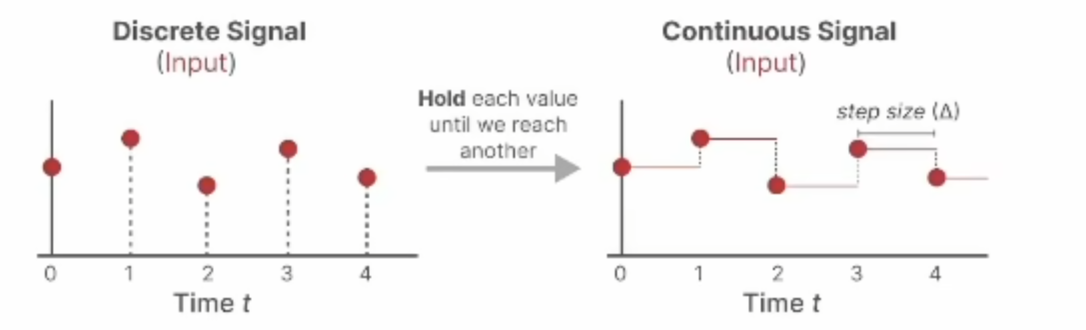
所谓离散化就是上图中连续的数据变成了离散化的数据
而零阶保持则是变成离散化以后,将数据变化变成了阶跃式的,保持当前当前时间的状态。
并行化处理与CNN
对应于最上面图中的Convolutional, 对于SSM而言,就是通过卷积实现了并行化。其核心思想就是使用CNN对时序数据进行建模,借助不同尺度的卷积核,从不同时间尺度上捕获时序特征。

k可以理解为一个伸缩窗口,当前状态可以用之前输出的加权和来表征,再把 $ h_t$代入到输出的式子,与卷积的公式进行对比。

在实际问题中,会对上述的AB矩阵进一步简化,会将其设置为对角阵,这就是结构化SSM,S4模型。
对于SSM模型,要记住,这里有两个强假设:线性+时不变,这两个假设极大的限制了其应用范围。而Mamba本质上就是对SSM模型的改进,其不再考虑这两个约束。
Mamba
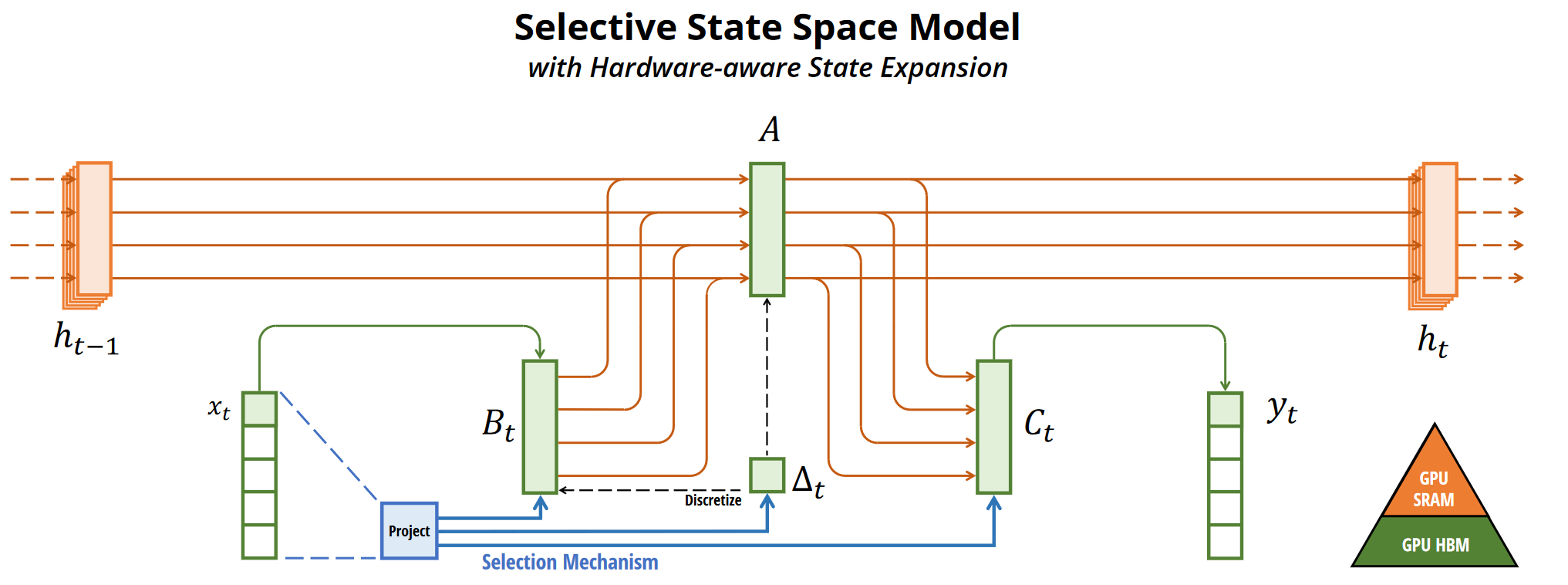
Mamba的设计机制让状态空间具备了选择性,同时在序列长度上实现了线性扩展。
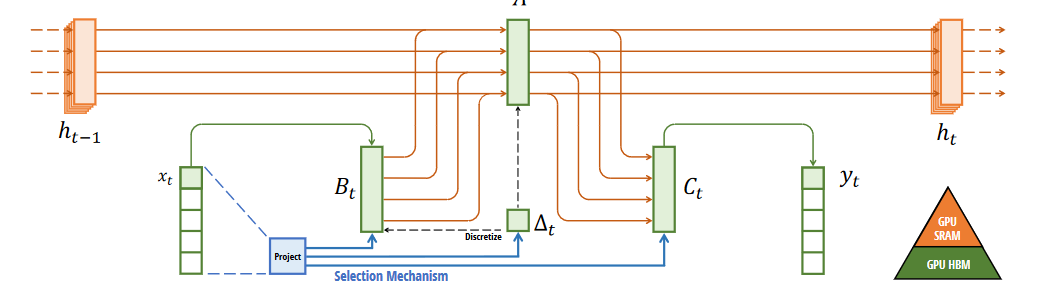
看这幅图的中间部分,BC都变成为了带有t的时变参数,A虽然没有加t,但其实也是时变的,因为会将Δt加入到A中,这里的Δt是一个非线性的,
Δt可以看作一个总开关,$B_t,C_t$就是旋钮。总开关 + 若干个旋钮 = 非线性时变系统
要解决的问题
序列建模的核心就是研究如何将长序列的上下文信息压缩到一个较小的状态中。
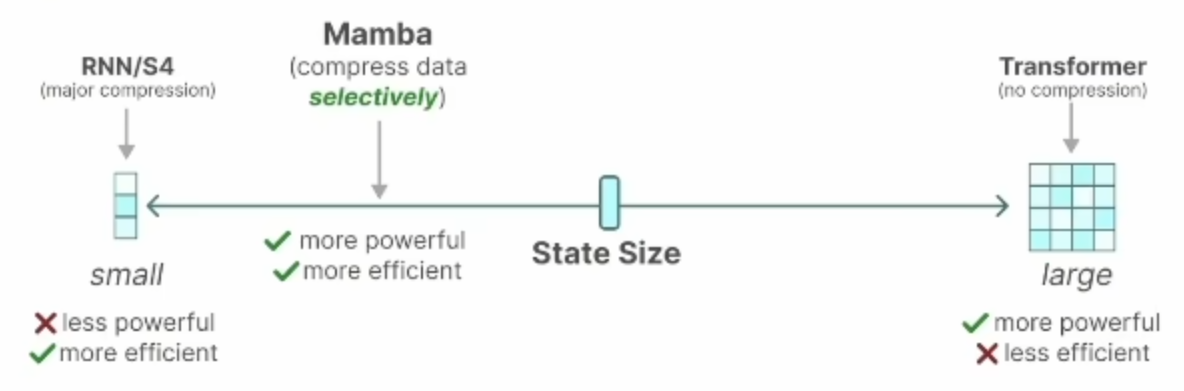
作者希望可以关注两种能力:
1.选择性复制任务(抓重点的能力)
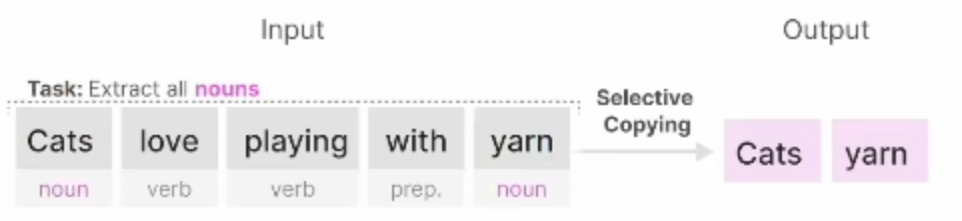
2.诱导头任务(上下文推理能力)
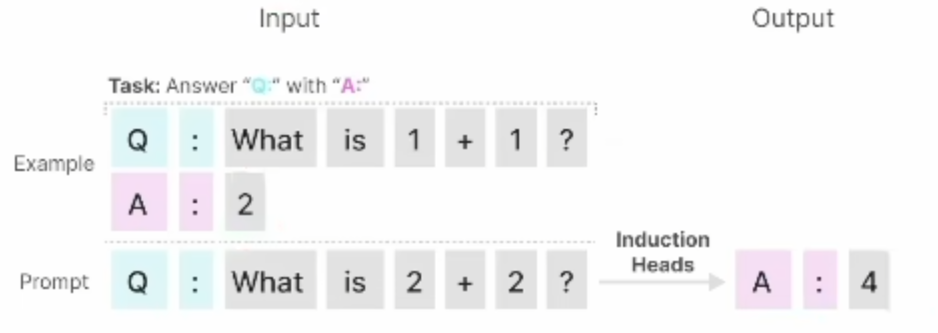
怎么增加选择性?
让B和C由原来固定的变为了可变的,根据$x_t$和其压缩投影学习可变参数。上图中蓝色部分(包括投影和连线)就是所谓的选择机制。目的是根据输入内容选择性地记忆和处理信息,从而提高对复杂序列数据的适应能力。

这里面的Δ是前面离散化计算时的参数,投影出来的三条蓝线其实就是$s_B,s_C和s_Δ三个选择函数$,共享一个投影模块(project),主要是为了实现参数共享和计算效率。
B:batch size,L:Sequence length,N:Feature dimension,D:input feature dimension。

上述所提到的$s_B(x)=Linear_N(x), s_C(x)=Linear_N(x), s_Δ(x)=Broadcast_D(Linear_1(x)), \tau_Δ=softplus$
这样设计的效果如图所示:
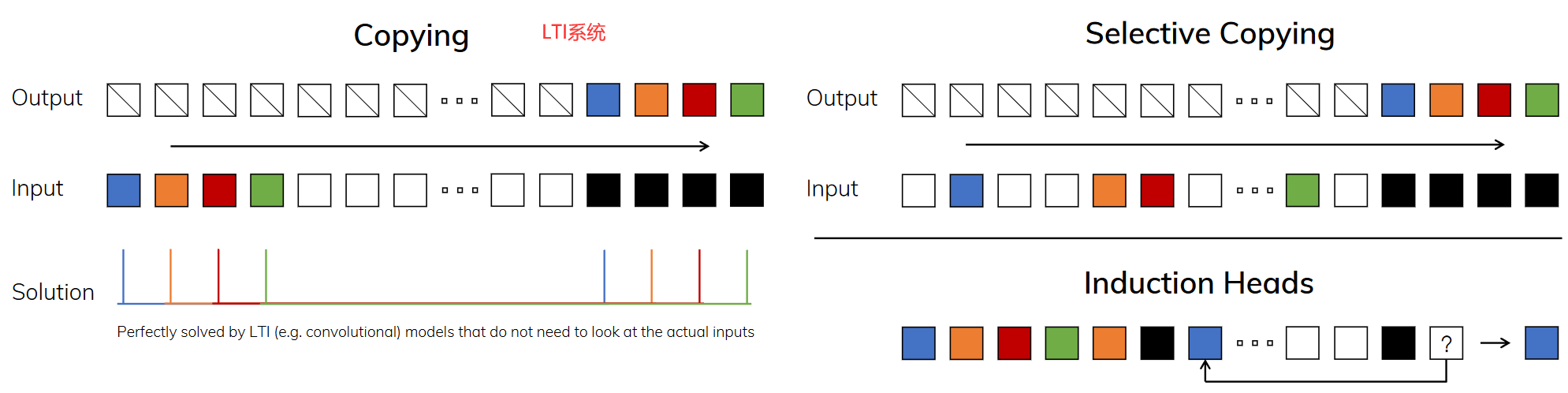
这也达到了注意力的效果。
核心原理



Mamba结构
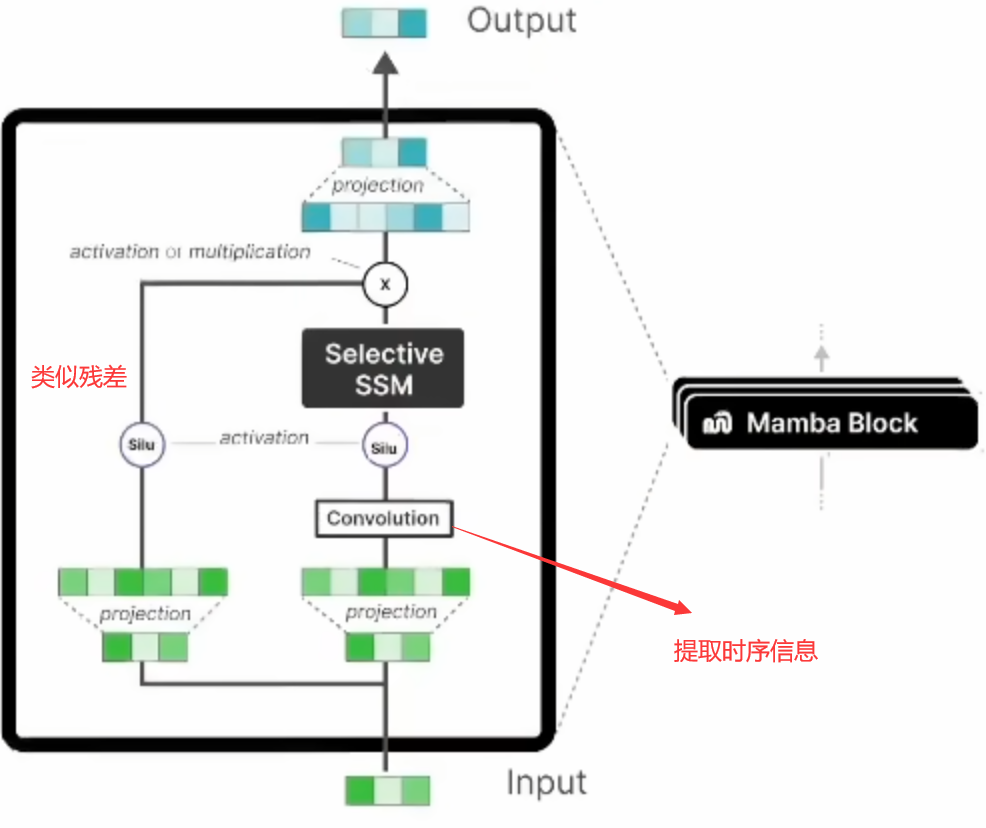
总结

补充
Part1: Transformer and RNN
对于transformer来说,无论接收到什么输入,它都可以回溯序列中的任何早期标记,从而推导出其自己的表示。尽管已经生成了一些token,但是当生成下一个token时,transformer任然需要重新计算整个序列的attention,这就导致了二次方的计算复杂度,当序列长度增加,其代价也就越大。
RNN有两个输入,一个是当前时间步的输入,另一个则是先前时间步的隐藏状态。利用这两个输入,RNN和产生下一个隐藏状态以及预测输出。当预测时,RNN避免重新计算先前所有的隐藏状态(这正是transformer想要做的)。这就意味着RNN在推理时非常快,因为其线性的尺度,也意味着在理论上RNN可以处理无限长的文本长度。
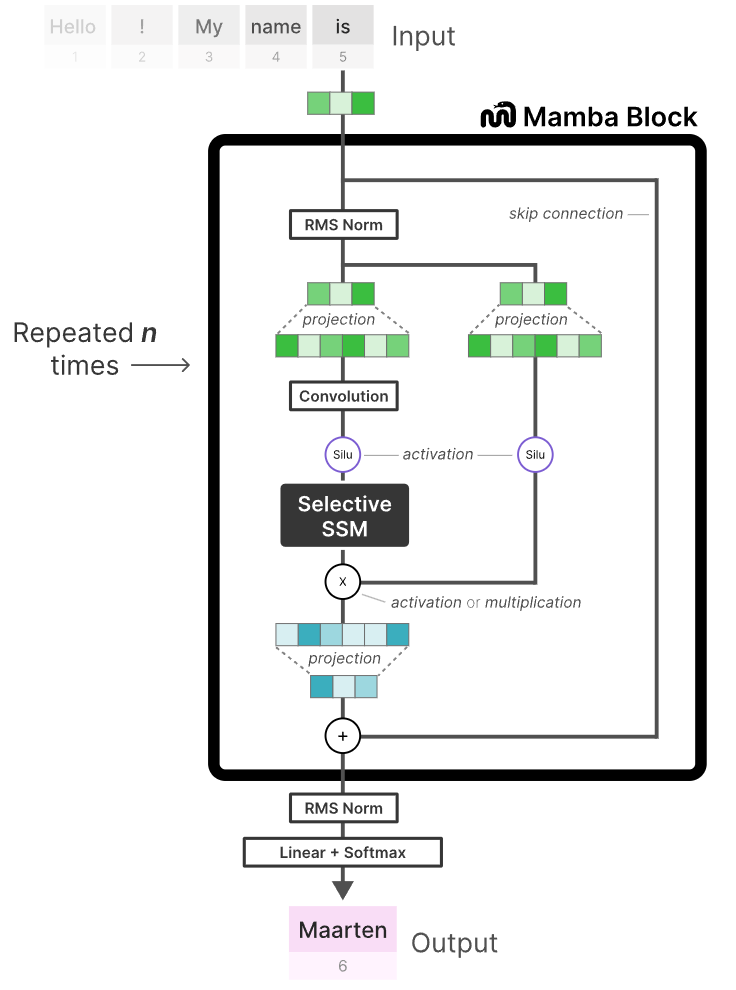
但是RNN也存在一些问题,因为他只考虑上一个时间步的隐藏状态,所以随着时间推荐,其会忘掉一些重要信息(如下图,当处理到“Maarten”时,会遗忘掉“Hello”);此外,RNN无法并行进行,因为它需要随着时间逐时间步的去进行处理。
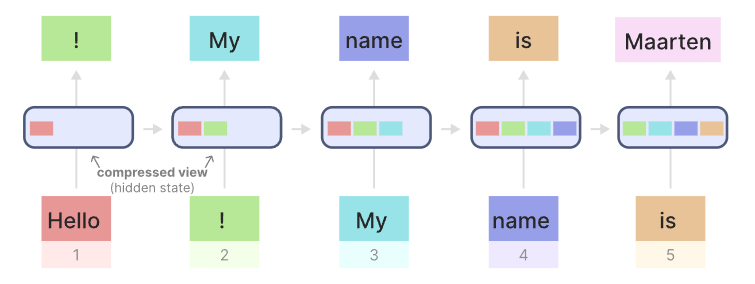
这时,RNN和Transformer所面临的优缺点就非常明显了。我们如何才能找到一种折中的方法呢?又可以像Transformer一样并行化处理,又可以随着序列长度进行线性扩展的推理。没错,就是Mamba。

Part2: The State Space Model(SSM)
状态空间就是能够充分描述一个系统所包含的最小变量数,其也是通过定义系统内可能的状态去数学化的代表一个问题。
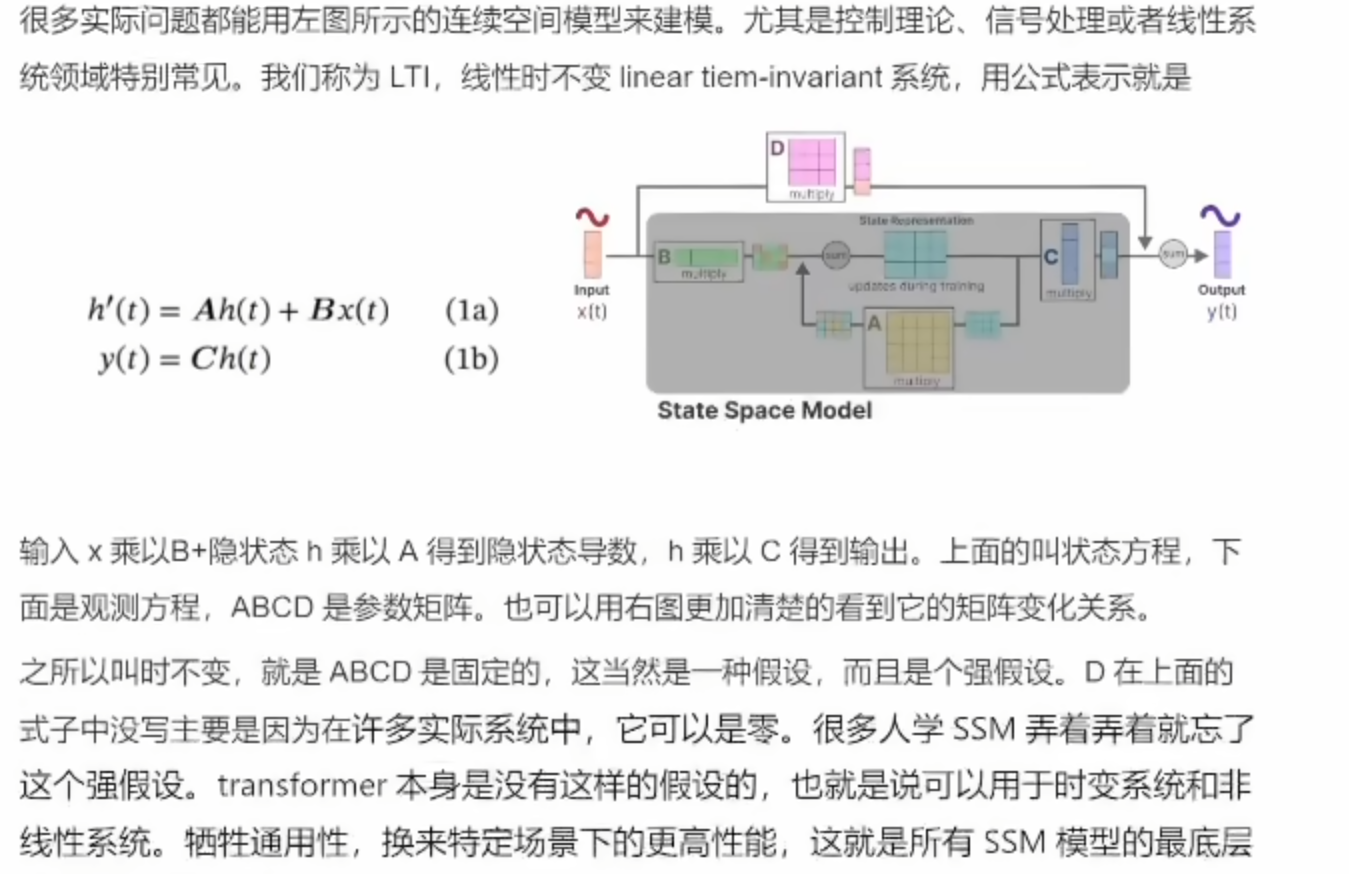
在传统的状态空间中,对于时间t,存在输入序列x(t),潜在的状态空间表示h(t),预测输出序列y(t)。

通过两个等式,就可以预测输出序列y(t)

这两个等式就是SSM的核心部分,(上面的式子被称为状态等式,下面的式子被称为输出等式)。
通过下图理解状态等式,可以看出隐藏状态是如何进行改变的(通过矩阵A),以及输入是如何影响状态(通过矩阵B)。
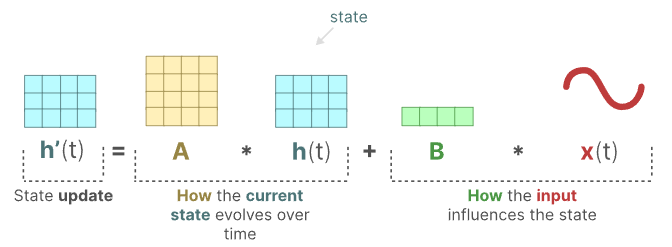
同理,对于输出等式,可以看出状态是如何转换成输出(通过矩阵C),以及输入如何影响输出(通过矩阵D)。
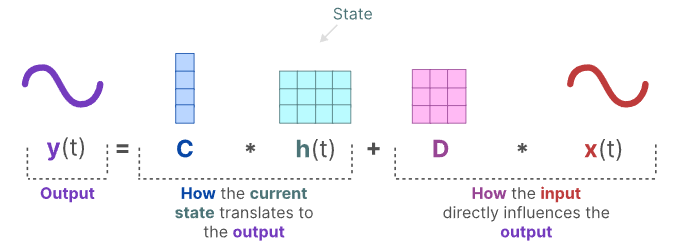
综上,我们可以得出以下结构(D也被叫做跳跃连接,这也是原因有时SSM会忽略掉这个跳跃连接)。
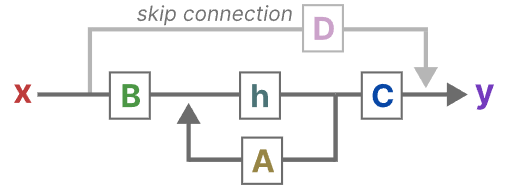
忽略跳跃连接以后的结构如下图所示。在这里我们仍然需要注意一点,输入和输出还都是连续的,但是我们经常处理的都是离散的token,所以就需要将连续变为离散。
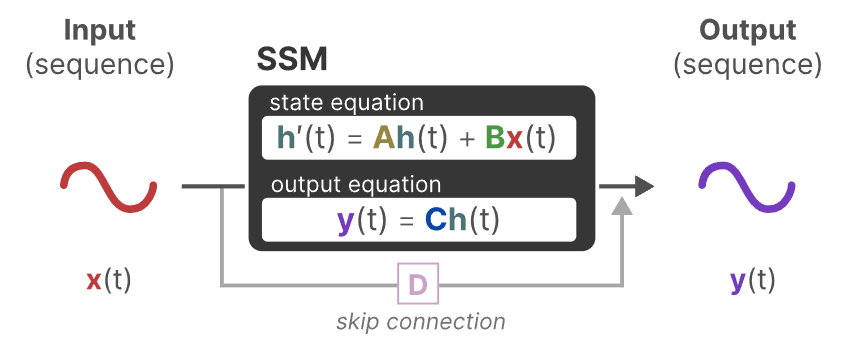
From a Continuous to a Discrete Signal
怎么将连续的信号变为离散的呢?这里使用的方法是零阶保持(Zero-order)。具体表现就是当我们接收到一个离散信号时,会一直保持其值,直到再次接受到一个新的离散信号,这个过程给SMM创造出了可以使用的连续信号。
零阶保持用数学公式的表达如下:
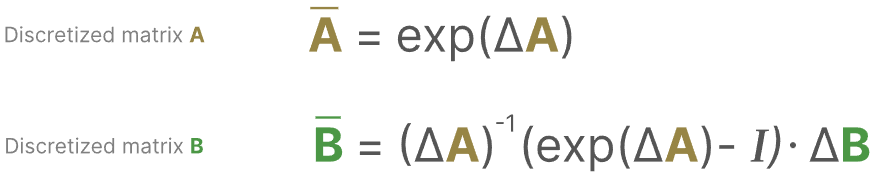
这里我看到了一个推导方法,可以帮助理解:
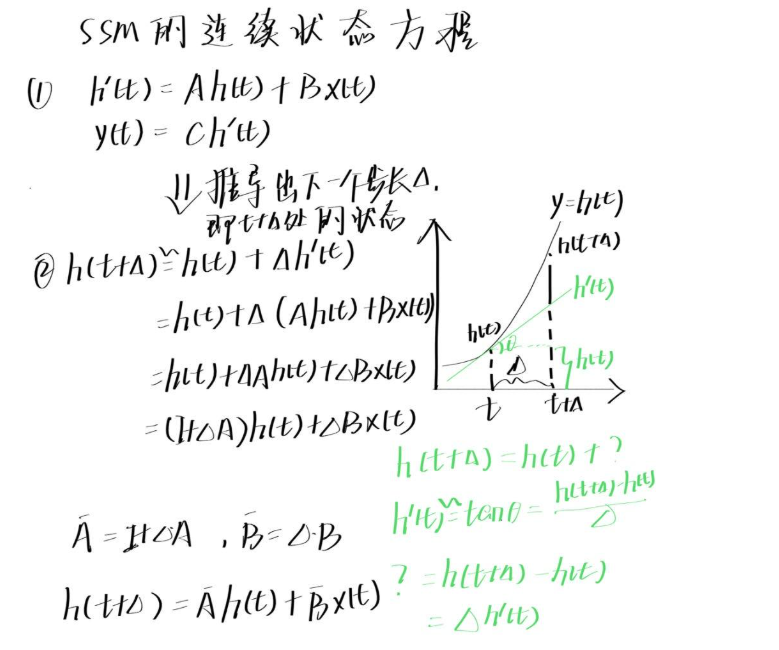

这个离散数值的保持时间由一个新的可学习的参数Δ来表示,其也代表了输入的分辨率。
现在我们有了连续的输入信号,就可以生成连续的输出,只需根据输入的时间步长对数值进行采样即可,采样值就是我们的离散化输出!!!
经过上述处理,我们可以从连续 SSM 变为离散 SSM,其表述方式不再是函数对函数,即 x(t) → y(t),而是序列对序列 $x_k → y_k$,如下图所示,这里的矩阵A和B目前代表模型的离散化参数。
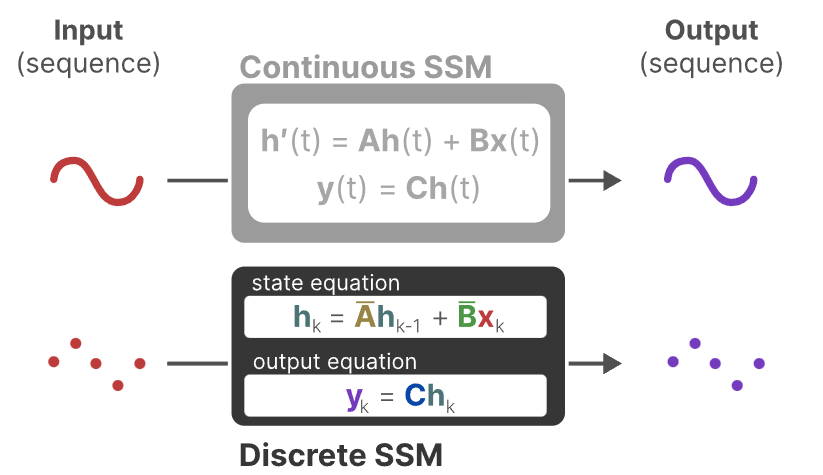
注意:在训练过程种,保存的是矩阵A的连续形式,而不是离散形式,在训练时,连续的表示形式会被离散化。
The Recurrent Representation && The Convolution Representation
现在,我们可以考虑如何在模型种进行计算。在每个时间步,我们计算当前输入如何影响先前的隐藏状态,并且计算所预测的输出。
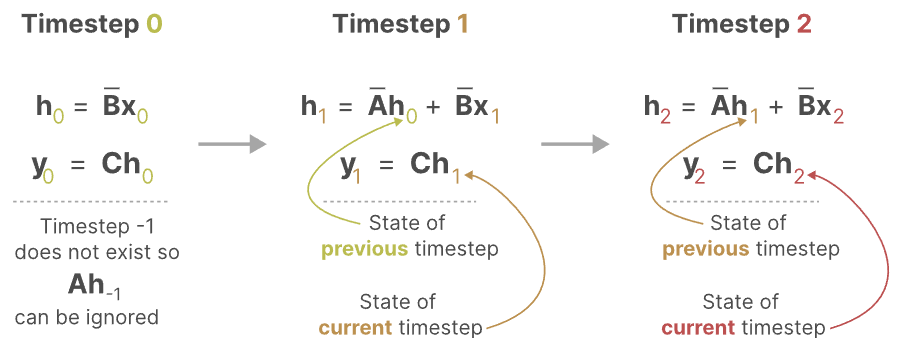
这是之前所看过的RNN是比较相似的,如下图:

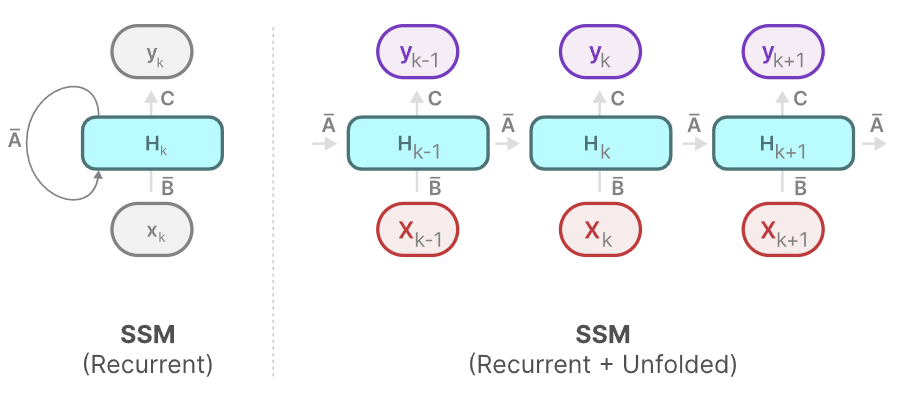
现在我们的计算方法类似RNN,其在推理时非常快速,但是训练时比较慢!
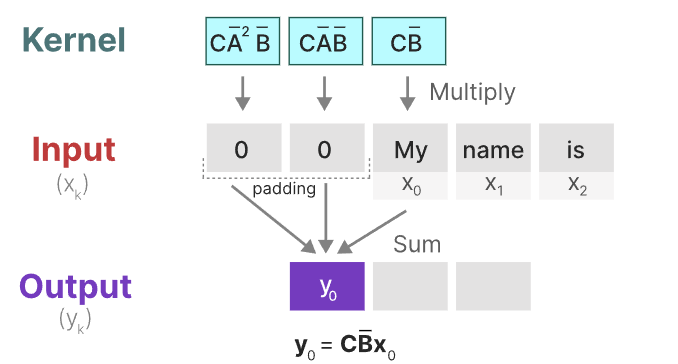
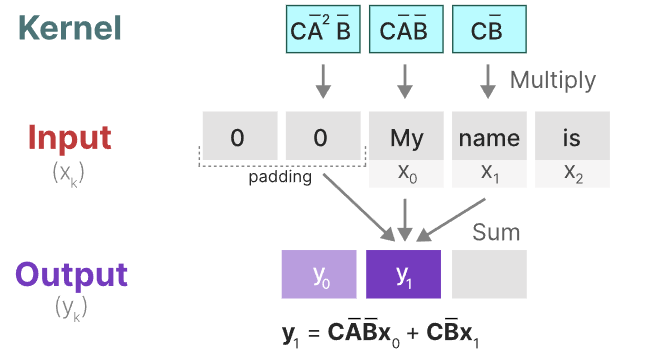
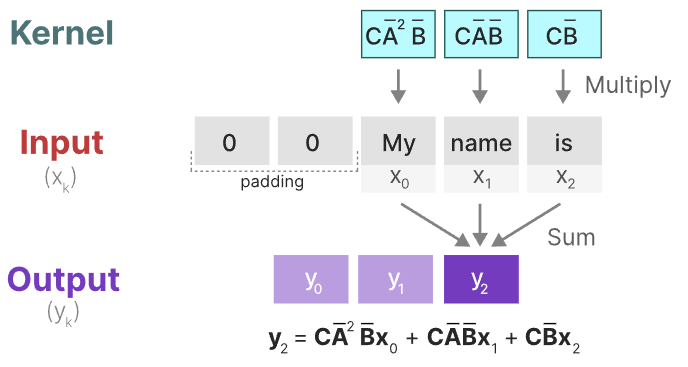
我们也可以使用另一种表示方法就是卷积,因为我们需要处理的是序列,而不是图像,所以需要使用的也就是1维卷积。
此时,我们使用的卷积核来自于SSM
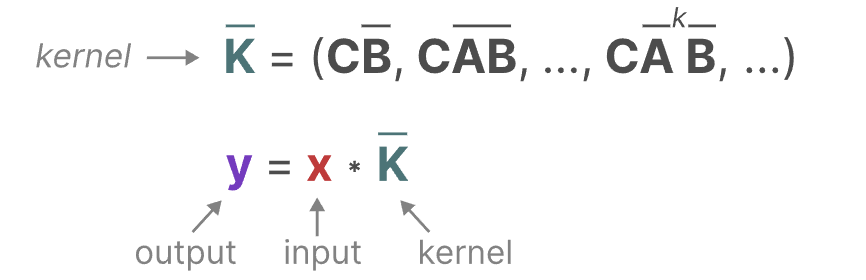
卷积核的推导如下所示(需要结合上面的状态等式和输出等式一起看):
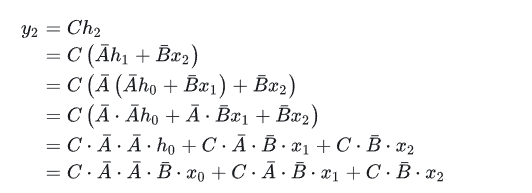
这样我们就以卷积的方式来并行计算。
HiPPO sequence
对于矩阵A来说,其是SSM中最重要的一个部分,因为其对上一个时间步的隐藏状态进行处理。矩阵A需要记住其之前所看过的所有标记之间的差异。那么该如何创建矩阵A,用于保留较大的内存去存储上下文呢?
这里使用HiPPO(High-order Polynomial Projection Operators),HiPPO尝试将所有的输入信号压缩成为一个系数向量。它可以很好地捕捉最近的token并且弱化之前的token,表示如下图。
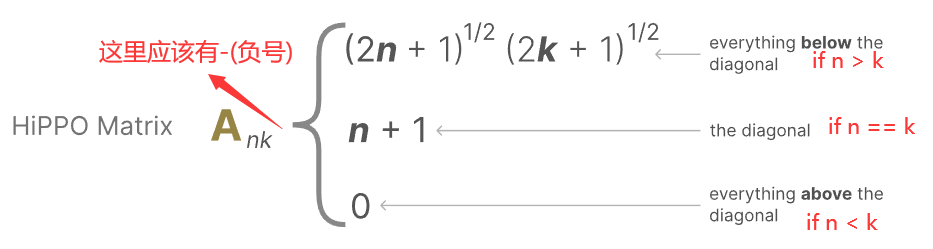
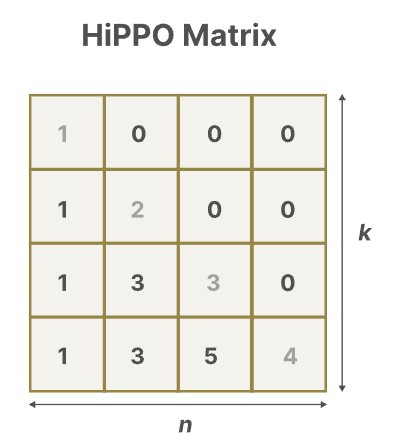
此时,我们的状态空间就从SSM转变成为了S4模型。其有一个重要特性就是线性时间不变性(Linear TIME Invariance, LTI)其意味着,对于一个给定的SSM,矩阵A, B, C都是保持固定的,是静态的,这也说明无论你向SSM中提供什么序列,A,B,C的值并不会随输入的改变而改变,这就说明暂时其并不具备内容感知的能力。
Part3: Mamba - A Selective SSM
对于Mamba来说,其有两个主要贡献:
- 选择扫描算法(selective scan algorithm): 这允许模型去过滤相关或者不相关的信息。
- 硬件感知算法(hardware-aware algorithm):通过并行扫描、核融合和重新计算高效地存储中间结果。
具体表述如下图: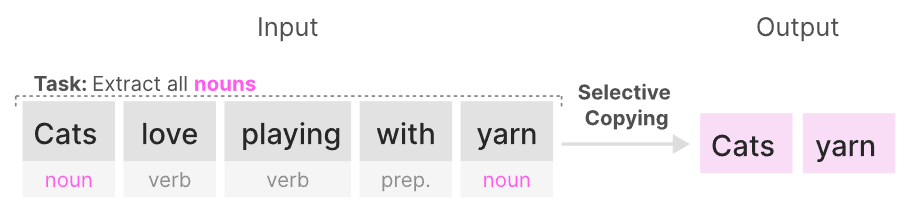
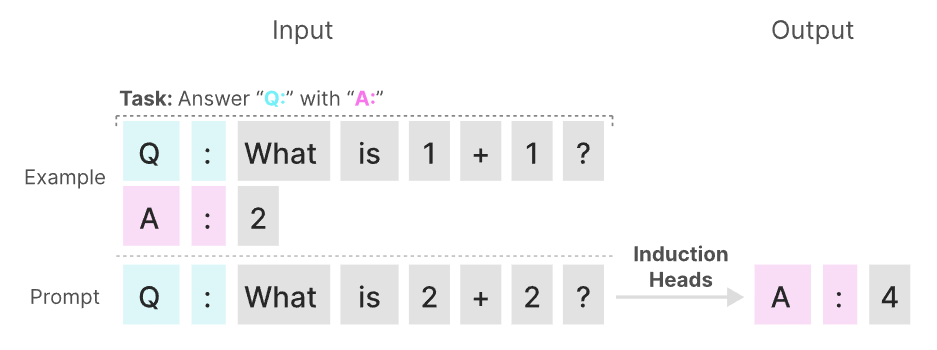
对于SSM以及S4,其对关注或忽略特定输入的内容等任务上表现并不好,在mamba中使用选择性复制(selective copying )和感应头(induction heads)。
由于我们上面提到的线性时间不变性导致了ssm无法进行内容感觉推理,但是我们希望ssm可以对输入进行推理,相比之下,transformer由于会根据输入序列动态改变注意力,其可以有选择地“注意”序列中的不同部分,所以在文本等任务上表现更好。这就说明矩阵A,B,C固有的LIM造成了无法进行内容感知的问题。
对于SSM和S4,A, B, C三个矩阵和输入独立,不会随着输入的改变而发生改变。与之相反地,mamba使A, B, C,甚至Δ都依赖于输入的序列长度和batch大小。
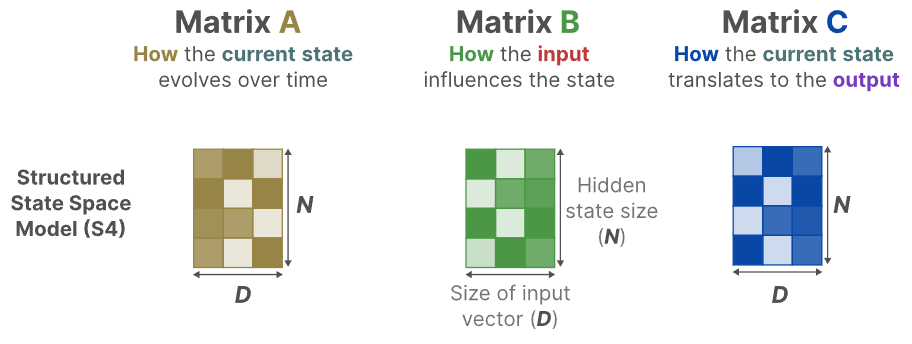
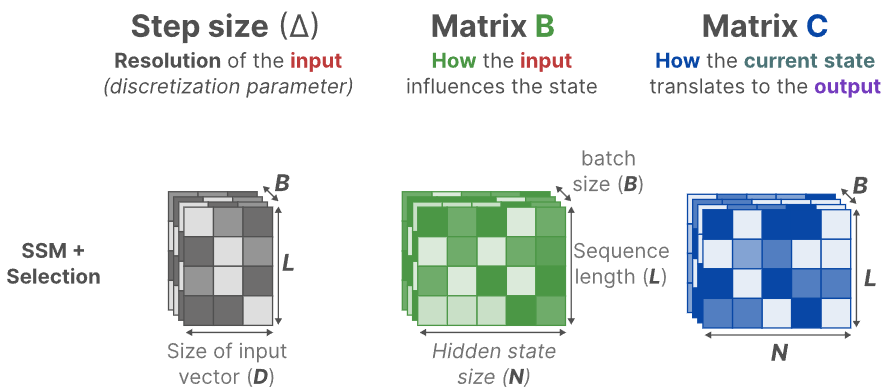
这意味着,对于不同的输入,就有不同的矩阵B和C,这就解决了所面临的无法进行内容感知的问题。
注意:矩阵A是静态的,因为我们希望状态是静态的,但是A又通过B,C影响,所以A又是动态的!!!
这些矩阵共同选择将哪些内容保留在隐藏状态,哪些内容忽略不计,因为它们现在依赖于输入内容。
较小的步长 ∆ 会导致忽略特定的单词,而更多地使用以前的上下文,而较大的步长 ∆ 则更多地关注输入的单词而不是上下文。
The scan operation
由于这些矩阵现在是动态的,因此无法使用卷积表示法进行计算,因为它假定了一个固定的核。我们只能使用递归表示法,而失去了卷积所提供的并行化功能。
每个状态都是前一个状态(乘以 A)加上当前输入(乘以 B)的总和。这就是所谓的扫描运算,可以用 for 循环轻松计算。相比之下,并行化似乎是不可能的,因为只有当我们拥有前一个状态时,才能计算出每个状态。然而,Mamba 通过并行扫描算法实现了这一点。
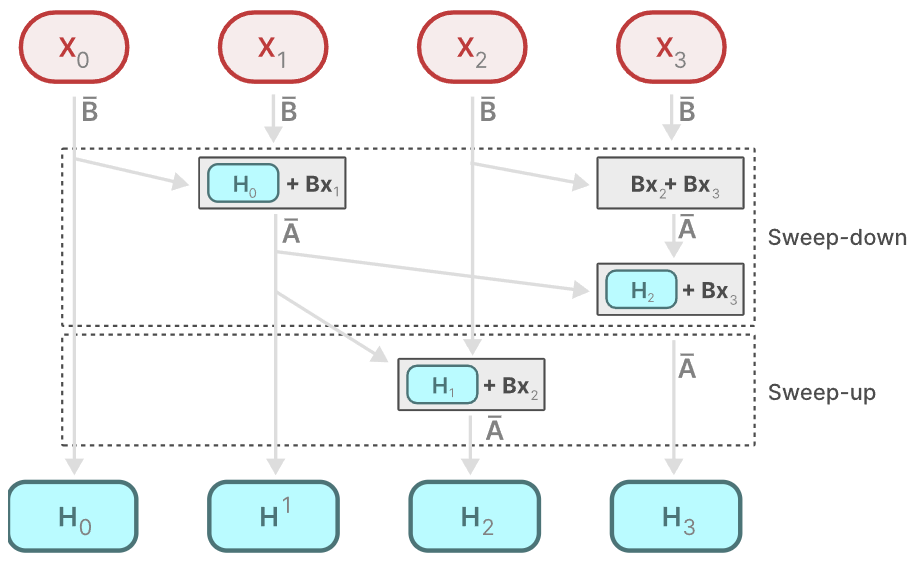
动态矩阵 B 和 C 以及并行扫描算法共同创建了选择性扫描算法
Hardware-aware Algorithm
最近推出的 GPU 的一个缺点是其小型但高效的 SRAM 与大型但效率稍低的 DRAM 之间的传输(IO)速度有限。经常在 SRAM 和 DRAM 之间复制信息会成为瓶颈。
Mamba 和 Flash Attention 一样,试图限制从 DRAM 到 SRAM 以及从 SRAM 到 DRAM 的次数。它通过内核融合来实现这一目标,使模型能够防止写入中间结果,并持续执行计算,直到完成为止。

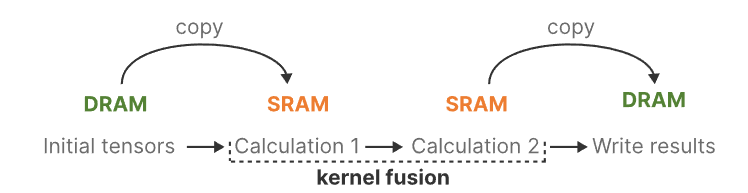
我们可以通过可视化 Mamba 的基本架构来查看 DRAM 和 SRAM 分配的具体实例:
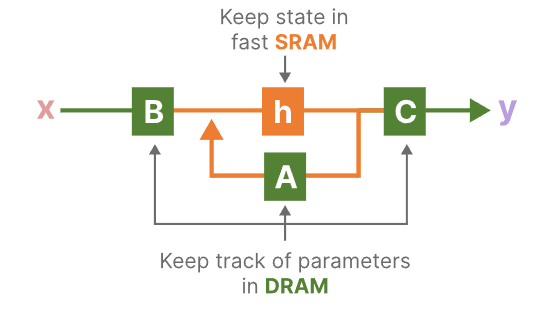
硬件感知算法的最后一个环节是重新计算。
中间状态不会被保存,但却是后向计算梯度所必需的。相反,作者在后向计算过程中重新计算了这些中间状态。
虽然这看起来效率不高,但比从相对较慢的 DRAM 中读取所有这些中间状态的成本要低得多。
整个Mamba的过程如下所示:
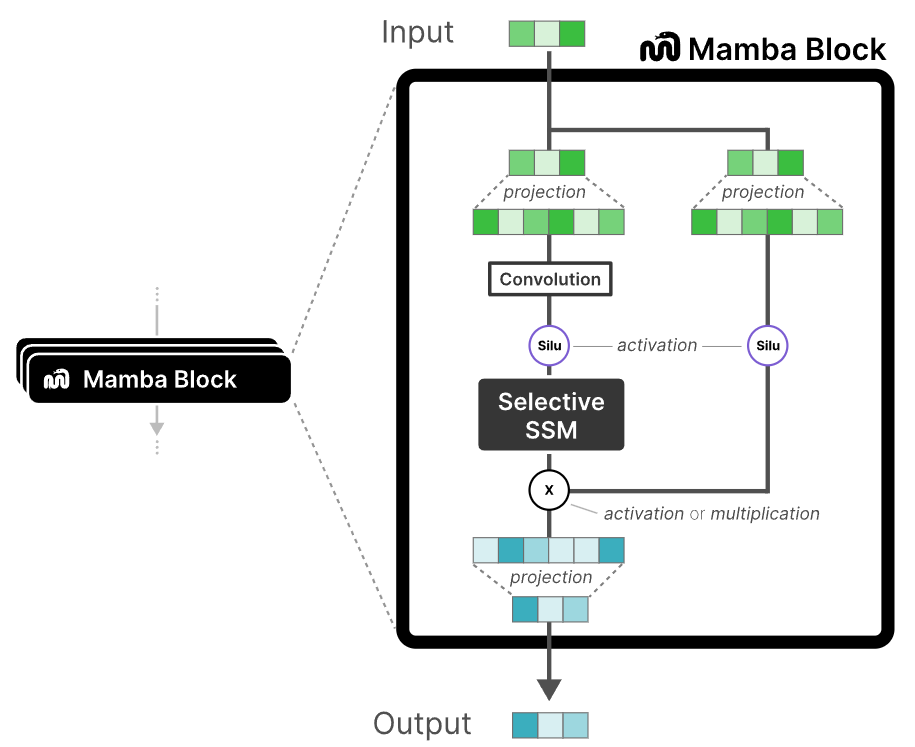
对于整个Mamba块的清晰表达如下图所示,它也可以通过堆叠多次来完成特定任务。