前言
这是第三遍读这篇论文了,同时自己计划对着源码把每次变换的形状弄明白,所以再看一遍论文的细节,并且对一些数据维度进行一下标注。
论文链接:[2211.08217] A Low-Shot Object Counting Network With Iterative Prototype Adaptation
我对论文代码进行了注释,并且对数据在变换过程中的形状变换进行了标注,可以在[PaperRecurrent/LOCA–A Low-Shot Object Counting Network With Iterative Prototype Adaptation at main · LengNian/PaperRecurrent](https://github.com/LengNian/PaperRecurrent/tree/main/LOCA--A Low-Shot Object Counting Network With Iterative Prototype Adaptation)中找到。此外,我修改了代码,使其可以成功运行,同时作者给出的代码是在多卡上运行,我进行修改后,可以在自己笔记本上单卡运行(按照作者给的训练指令,只需把卡数变成1即可)。
整体结构
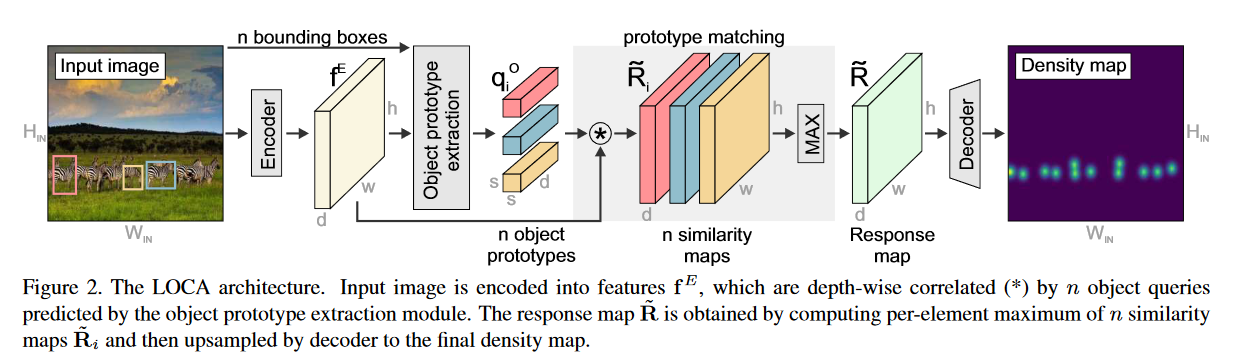
(1) 输入图像的大小调整为$ H_{in} \times W_{in}$,使用ResNet50编码,从ResNet50第二、三、四个block中提取到的多尺度特征也调整大小到$ h \times w$,并使用1*1卷积将通道变为d维,然后通过一个全局自注意力块(3层的Transformer encoder)加强编码特征,产生了图像特征$f^E \in R^{h \times w \times d}$;
(2) 将边界框和图像特征$f^E$送入物体原型提取模块(OPE),就会得到n个物体原型$ q_i^{O} \in R^{s \times s \times d}$,图像特征和原型深度关联得到了多通道的相似性张量$\tilde{R}_i, \tilde{R}_i = f^E * q_i^O $。通过每个通道,每个像素进行最大值运算,将n个单独的相似性向量$\tilde{R}$融合在一起形成一个联合相应张量$\tilde{R} \in R^{h \times w \times d}$;
(3) 使用一个回归头预测最后的二维密度图$R \in R^{H_{IN} \times R_{IN}}$。回归头由三个卷积层组成,包括128,64,32通道,每一个卷积层后面跟随一个Leaky ReLU和一个2$\times$双线性采样层和一个线性1*1卷积层,后面再跟一个Leaky ReLU。
Object prototype extraction module(OPE)
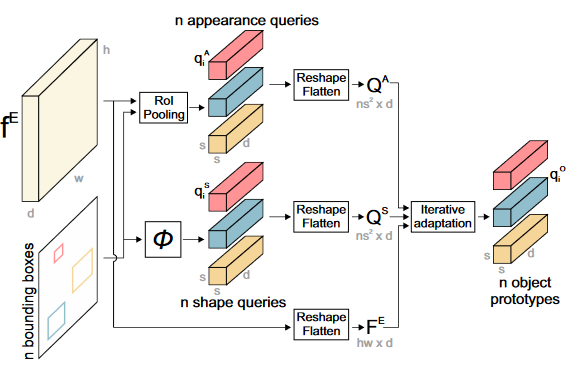
OPE使用图像$f^E和对应的n个边界框$${b_i}_{i=1:n}$生成n个对象原型$ q_i^{O} \in R^{s \times s \times d}$
获得外观和形状查询
外观查询$q_i^A \in R^{s \times s \times d}$被提取通过RoI池化操作从图像特征$f^E$中提取,转换为s*s的张量。因为池化把特征图转化为相同大小,所以形状信息在这个过程中被忽略了。形状信息用示例原型的高和宽进行初始化,第i个边界框对应的形状查询是通过将其宽度和高度进行非线性映射成为高维张量($R^2 -> R^{s \times s \times d}$),即$q_i^S = \phi([b_i^W, b_i^H])$**(这里说每个形状信息是通过初始化示例的高和宽,所以相当于就是按照边界框的高和宽进行初始化。)**,映射$\phi$是一个三层的FFN组成,每个linear后有一个ReLU。
外观和形状查询注入到对象原型(通过迭代适应模块)
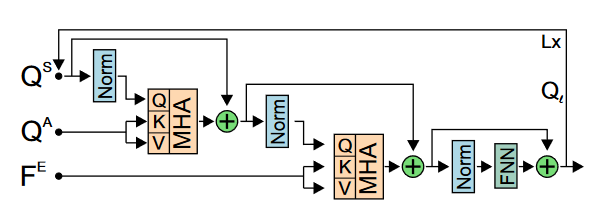
首先将形状查询调整形状成为一个矩阵$Q^S \in R^{ns^2 \times d}$,外观查询和特征图也同理得到$ Q^A \in R^{ns^2 \times d}$和$F^E \in R^{hw \times d}$。
少样本
然后通过一个循环的交叉注意力块将外观查询和和形状查询注入到对象原型中,在这里的交叉注意力块包括形状查询和外观查询进行多头交叉注意力以及特征图和上一个多头交叉注意力的结果再进行多头交叉注意力,最后再通过前馈传播网络,得到一次注入的结果$Q^{l} \in R^{ns^2 \times d},l \in {1,…,L}$,如此迭代L轮。最后迭代适应模块的输出$Q^L$重新调整形状为一组n个对象原型$q_i^O \in R^{s \times s \times d}$。
零样本
如果是零样本的情况下,就没有形状查询和外观查询,所以就初始化一个可以学习的参数来代替最初的$Q^l$。
训练损失
同大多数的工作一样,使用L2 loss,但是这里增加了一个辅助损失,用于更好地监督迭代适应模块的训练。
(从原文的图中可以看出,迭代适应模块的结果经过一系列最大化的操作,就得到了响应图。再经过回归头就得到了预测密度图,所以这里把每次迭代适应的输出通过max和regress head就得到了当前迭代输出的结果所对应的预测密度图,利用这个密度图与ground truth进行L2 loss,这就是辅助损失)
最终的损失就是$ L = L_{OSE} + \lambda_{AUX}L_{AUX}$
实验细节
$H_{IN} = W_{IN} = 512, h = w = 64, d=256 $
迭代适应模块中的MHA包含8个头,隐藏维d=256,FFN的隐藏维为1024;进行3次迭代,即L=3,s = 3
