前言
最近看了一篇人群计数的论文,并进行了复现,主要是用于自己去了解人群计数的整个流程。
本文不是对论文进行翻译,只是对文章进行简略的总结,并对部分内容写出我的理解,主要是将自己阅读和复现过程中遇到的些问题在这里记录一下,希望可以帮助到有需要的人,同时,本文的内容均为个人理解,如若有误,欢迎在评论区或者邮件指正。
源代码 :crowdcount-mcnn:Single Image Crowd Counting via MCNN (Unofficial Implementation) - GitCode
环境调试
可以下载作者开源的代码,但是作者当时上传的代码有些老,所以会有很多不兼容的问题需要自己一步一步去调试。
在文章[MCNN] Crowd Counting 人群计数 复现过程记录_mcnn复现-CSDN博客中对调试的内容写的非常详细,所以本文在此不赘述。
我将自己调试好的程序上传到了Github,大家也可以自行下载PaperRecurrent/crowdcount-mcnn-master at main · LengNian/PaperRecurrent (github.com)
读论文
该论文提出一种简单但是有效的多列卷积神经网络(MCNN),每列的感受野大小不同,用于提取不同的特征。同时,提出了Shanghai Tech数据集。
MCNN输入的是图像,会输出对应的人群密度图,通过对该密度图进行积分,就可以得到对应的人群数量。
因为透视失真的问题,简单的来说就是图像中近大远小的问题,会导致图像中人群的头部大小各异,所以使用不同尺度的卷积核才能捕捉到不同尺寸的人群密度特征。MCNN结构图如图所示。
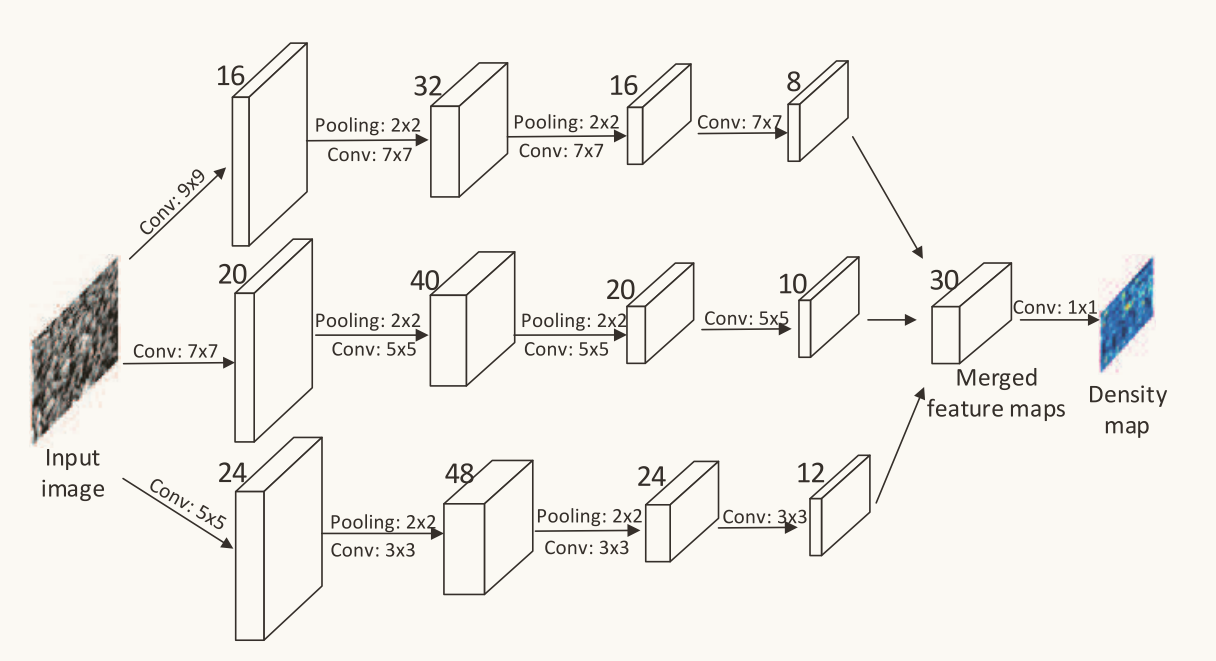
作者在训练的时候对数据进行了增强,对于训练集数据,作者使用matlab对每张图片随机裁剪9次,论文中提到对训练样本进行下采样1/4,这里要注意的是,是对图像的长宽缩减到原来的1/4,而不是面积,面积实际缩减为了原来的1/16。如图所示。
全篇文章中,到时候最想不明白的就是3.2 Shanghai Tech dataset中的Comparison of different loss functions。这里讲了两种不同的方方式,一种是将图像直接映射到图像中的总人头数(我的理解就是其输出内容就为总人头数),另一种是将图像映射为密度图(也就是模型的输出就是与输入对应的密度图)。
对于公式(1),F(X,Θ)就是模型所输出的密度图,通过一个二重积分得到的就是该密度图上的总人数,$ z_i$表示的就是第i个图像中的总人数,通过将预测出来的总人数减去实际总人数,并平方等步骤计算损失函数。
源码理解
这部分,我会记录一些我在读源码时一些难理解的点。
第一处是data_loader.py中对数据预处理的部分,即if self.preload:中的部分
if self.gt_downsample:
wd_1 = wd_1//4
ht_1 = ht_1//4
den = cv2.resize(den,(wd_1,ht_1))
den = den * ((wd*ht)/(wd_1*ht_1))
else:
den = cv2.resize(den,(wd_1,ht_1))
den = den * ((wd*ht)/(wd_1*ht_1))我当时最不理解的就是 den = den * ((wdht)/(wd_1ht_1))这句代码,这里是对密度图的值进行了改变。
密度图中的每个像素值通常代表了一定区域内的人群密度,对密度图的尺寸修改后,会影响到整个图像所表示的总密度。为了补偿这种影响,需要调整新图像中每个像素的值,使其所代表的总人群密度与原始图像相同,常用方法就是乘一个比例因子,这个比例因子就等于原始图像面积 / 新图像面积。
举个例子,比如有一张图像大小为10 * 10,表示100个人,相当于100个像素表表示100个人,平均下来就是每个像素代表一个人。当对图像缩小2倍,即5 * 5,此时相当于25像素表示100个人,那么平均下来就是一个像素四个人,很明显如果继续按照原来的密度图进行计算,会出错,此时乘一个比例因子,即100/25=4,25*4=100。由此可见通过比例因子的调整,大小修改后的密度图表示的内容与之前是相同的。
第二处是crowd_count.py中的内容
class CrowdCounter(nn.Module):
def __init__(self):
super(CrowdCounter, self).__init__()
self.DME = MCNN()
self.loss_fn = nn.MSELoss()
@property
def loss(self):
return self.loss_mse
def forward(self, im_data, gt_data=None):
im_data = src.network.np_to_variable(im_data, is_cuda=True, is_training=self.training)
density_map = self.DME(im_data)
if self.training:
gt_data = src.network.np_to_variable(gt_data, is_cuda=True, is_training=self.training)
self.loss_mse = self.build_loss(density_map, gt_data)
return density_map这里使用了property装饰器, 其装饰的函数的返回值可以直接被调用, 这也是为什么虽然__init__中虽没有定义self.loss_mse, 但是为什么后面可以调用。
第三处是data_preparation/create_training_set_shetch.m中的内容。
论文中说了对训练集进行增强的过程就是将每张图片随机截取9张原图四分之一的图像作为训练集。在代码中,这里是对长款取了八分之一,我的理解这个八分之一的长宽其实就是属于从中间往左边截八分之一,从中间往右边截八分之一,这样合起来就相当于是截取了四分之一。下图是我所理解的取样四分之一。
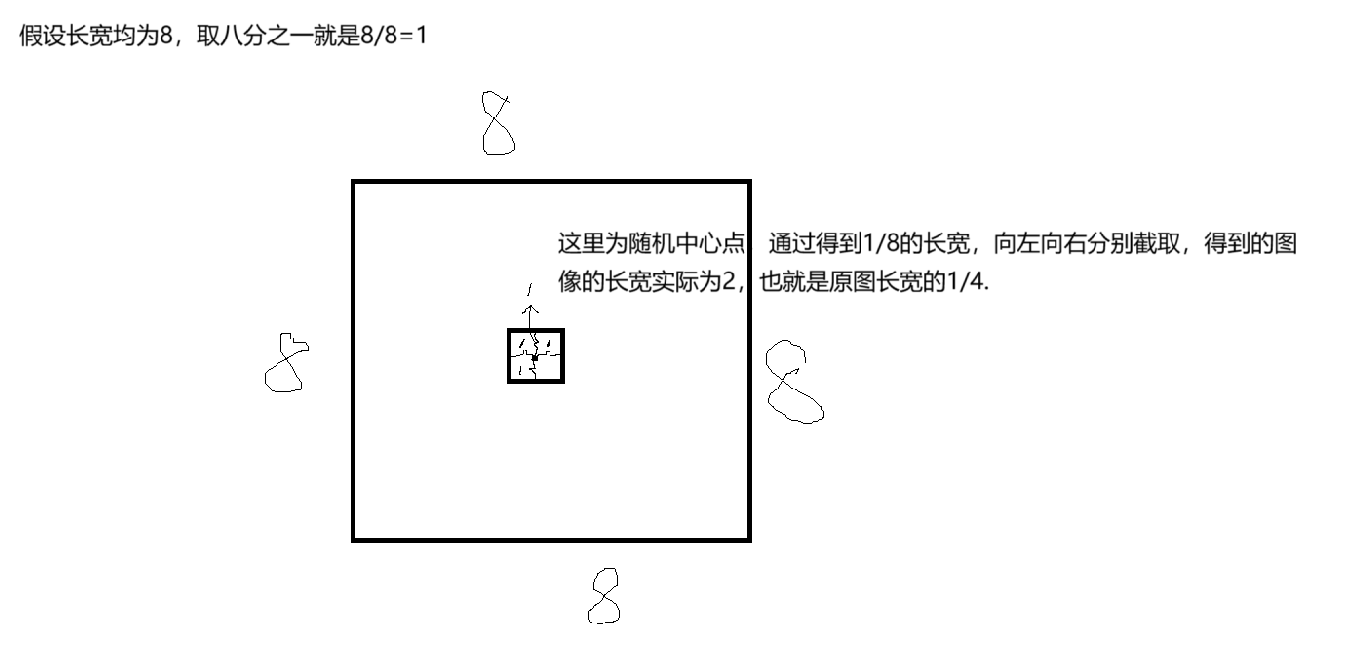
相应的代码如下
for idx = 1:num_images
i = indices(idx);
if (mod(idx,10)==0)
fprintf(1,'Processing %3d/%d files\n', idx, num_images);
end
load(strcat(gt_path, 'GT_IMG_',num2str(i),'.mat')) ;
input_img_name = strcat(path,'IMG_',num2str(i),'.jpg');
im = imread(input_img_name);
[h, w, c] = size(im);
if (c == 3)
im = rgb2gray(im);
end
wn2 = w/8; hn2 = h/8;
wn2 =8 * floor(wn2/8);
hn2 =8 * floor(hn2/8);
annPoints = image_info{1}.location;
if( w <= 2*wn2 )
im = imresize(im,[ h,2*wn2+1]);
annPoints(:,1) = annPoints(:,1)*2*wn2/w;
end
if( h <= 2*hn2)
im = imresize(im,[2*hn2+1,w]);
annPoints(:,2) = annPoints(:,2)*2*hn2/h;
end
[h, w, c] = size(im);
a_w = wn2+1; b_w = w - wn2;
a_h = hn2+1; b_h = h - hn2;
im_density = get_density_map_gaussian(im,annPoints);
for j = 1:N
x = floor((b_w - a_w) * rand + a_w);
y = floor((b_h - a_h) * rand + a_h);
x1 = x - wn2; y1 = y - hn2;
x2 = x + wn2-1; y2 = y + hn2-1;
im_sampled = im(y1:y2, x1:x2,:);
im_density_sampled = im_density(y1:y2,x1:x2);但是这段代码中我还有一处不理解的就是
if( w <= 2*wn2 )
im = imresize(im,[ h,2*wn2+1]);
annPoints(:,1) = annPoints(:,1)*2*wn2/w;
end
if( h <= 2*hn2)
im = imresize(im,[2*hn2+1,w]);
annPoints(:,2) = annPoints(:,2)*2*hn2/h;w不应该是恒大于2*wn2的嘛,因为wn2是w/8,即使有w特别小的情况,wn2被下取整变为了0,所以我对这里的判断不是很理解。
以上就是阅读MCNN论文中的一些记录,如果大家发现什么问题欢迎在评论区指正或者发邮件交流。
