DeepFool原理

DeepFool算法是一种基于梯度的攻击方法，这种方法看到以后感觉有点像支持向量机。这种方法在论文[1511.04599] DeepFool: a simple and accurate method to fool deep neural networks (arxiv.org)中提出。

对于线性二分类问题，有

$$ f(x) = w^Tx+b \tag{1} $$
分类边界定义为
$$ \mathscr{F} = x : f(x) = 0 \tag{2} $$
假设此时有 <>div $$ f(x_0) > 0 \tag{3} $$ <>/div 这里的x位于直线的下方。我们希望可以添加扰动r，使分类器出错，即
$$ f(x_0 + r) < 0 \tag{4} $$ <>/div 我们想要扰动成功，就是要跨过这个分类平面，

如何添加扰动可以实现这样的目的呢？如下图所示

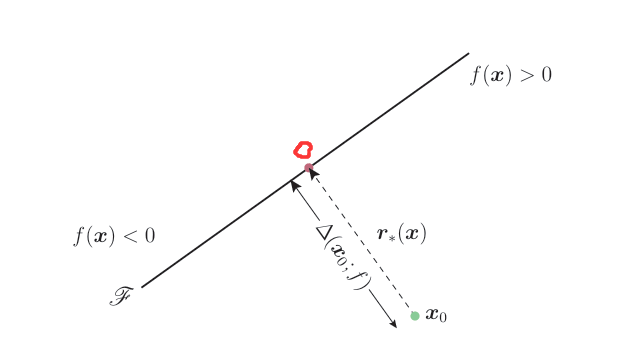
过x0做f(x)的垂线，假设交于点O，点x0与O之间的距离就是点x0到分类边界之间的最短距离，其方向也就是扰动的方向，沿该方向进行扰动，可以保证扰动最小。

我们把这个距离记为r*(x0)，即：

$$ r_*(x_0): = argmin \Vert r \Vert_2 \tag{5} \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad subject \; to\; sign(f(x_0+r))\neq sign(f(x_0)) \\ \qquad\quad =-\frac{f(x_0)}{\Vert \omega \Vert_2^{2}}w. $$
在论文中也给出了二分类方法的伪代码

对于多分类问题，定义fk(x)是分类器在第k类上的概率，那么

$$ \widehat{k}(\bold{x}) = arg \; \underset{k}{max} \; f_k(\bold{x}) \tag{6} $$
就表示分类的最终标签。同二分类的思想一致，**我们要求出x0到每个分类边界的距离（K个类），将距离最短的作为扰动，其方向也就是最终的扰动方向**
$$ \widehat{l}(x_0) = \underset{k \neq \widehat{k}(\bold{x_0})}{arg \; min} \frac{\vert f_k(\bold{x_0}) - f_{\widehat{k}}(\bold{x_0}) \vert}{\Vert \bold{\omega}_k - \bold{\omega}_{\widehat{k}(\bold{x_0})} \Vert_2}. \tag{7} $$
此外，还需要注意的是，在多分类中，将分类边界定义为
$$ \mathscr{F}_k = x : f_k(x) - f_{\widehat{k}(x_0)}(x) = 0 \tag{8} $$
论文中也给出了伪代码：

Pytorch实现

DeepFool核心代码参考自Github(github.com)，其中，我对代码进行了部分修改，比如将部分已弃用函数修改，输入图像维度修改等。并且逐句代码增加了注释。

def DeepFool(image, label, net, device, num_classes=10, max_iter=50, overshoot=0.02):
    # 源代码中这里输入的image为H*W*3,而我这里为B*H*W*C

    image = image.to(device)
    
    # 源代码这里增维了一次, 我这里有batchsize所以不需要进行增维
    # f_image为经过模型的对各个类别的预测
    # f_image = net.forward(Variable(image[None, :, :, :], requires_grad=True)).data.cpu().numpy().flatten()
    f_image = net(image).data.cpu().numpy().flatten()  # shape:[1, 10] -- [10]


    # argsort(排序,返回在原数据中的索引，从小到大排,使用[::-1]变为了从大到小)
    I = (np.array(f_image)).flatten().argsort()[::-1]

    I = I[0:num_classes]
    # 模型实际预测的标签,我这里改为该数据的真实标签
    # label = I[0]

    # 获取输入图像的形状
    # 源代码输入image是H*W*C,我这里需要降维
    # input_shape = image.cpu().numpy().shape
    input_shape = image.squeeze(dim=0).cpu().numpy().shape
    pert_image = copy.deepcopy(image)

    w = np.zeros(input_shape)  # shape[1, 28, 28]
    r_tot = np.zeros(input_shape) # shape[1, 28, 28]
    
    loop_i = 0
    # 源代码这里又增加一个维度，我只需要直接深拷贝原始图像即可
    # x = Variable(pert_image[None, :], requires_grad=True)
    x = torch.Tensor(pert_image)
    x.requires_grad = True

    fs = net(x)  # fs shape: [1, 10]
    # fs这里的shape是[1,10],所以这里使用fs[0, I[k]],也可以把fs降维成[10]
    # 这是把预测的概率值从大到小放到fs_list中了
    fs_list = [fs[0, I[k]] for k in range(10)]

    # k_i表示添加扰动以后预测的类别,这里对k_i进行初始化
    k_i = label

    while k_i == label and loop_i < max_iter:
        # pert用于存储最小的扰动
        pert = np.inf
        # 计算该预测标签在输入数据x处的梯度
        fs[0, I[0]].backward(retain_graph=True)
        grad_orig = x.grad.data.cpu().numpy().copy()

        for k in range(1, 10):
            # 将模型中所有参数的梯度清零
            zero_gradients(x)
            # x.grad.zero_()

            # 计算第k个标签在输入数据x处的梯度
            fs[0, I[k]].backward(retain_graph=True)
            cur_grad = x.grad.data.cpu().numpy().copy()

            # 计算第k个类别和应预测类别在x梯度的差异,也是扰动应该添加的方向
            w_k = cur_grad - grad_orig
            f_k = (fs[0, I[k]] - fs[0, I[0]]).data.cpu().numpy()

            # 计算了梯度向量w_k的L2范数,pert_k越小，扰动越小，攻击越有效
            pert_k = abs(f_k) / np.linalg.norm(w_k.flatten())

            # 选择最小扰动进行保存
            if pert_k < pert:
                # 需要移动的距离
                pert = pert_k
                # 扰动方向
                w = w_k
        
        r_i = (pert + 1e-4) * w / np.linalg.norm(w)
        # 累加到总扰动上
        r_tot = np.float32(r_tot + r_i)

        pert_image = image + (1 + overshoot) * torch.from_numpy(r_tot).cuda()

        # x = Variable(pert_image, requires_grad=True)
        x = torch.Tensor(pert_image)
        x.requires_grad = True

        fs = net(x)
        # k_i表示预测标签
        k_i = np.argmax(fs.data.cpu().numpy().flatten())

        loop_i += 1
        
    # 放大扰动
    r_tot = (1+overshoot) * r_tot

    return r_tot, k_i, pert_image

训练+攻击完整代码

这里的代码是从训练模型到进行对抗样本生成到可视化的完整过程。

import torch
import numpy as np
import torchvision
import random
import copy
from tqdm import tqdm
import torch.nn as nn
from torchvision import datasets, transforms
from torchsummary import summary
import matplotlib.pyplot as plt
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torch.autograd.gradcheck import zero_gradients

# 设置随机种子
torch.manual_seed(20)
# 设置GPU随机种子
if torch.cuda.is_available():
    torch.cuda.manual_seed(20)

np.random.seed(20)
random.seed(20)

# 搭建LeNet模型
class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()

        # 卷积层
        self.conv = nn.Sequential(
            nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2),
            nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2)
        )

        # 全连接层
        self.fc = nn.Sequential(
            nn.Linear(in_features=16 * 5 * 5, out_features=120),
            nn.ReLU(),
            nn.Linear(in_features=120, out_features=84),
            nn.ReLU(),
            nn.Linear(in_features=84, out_features=10)
        )

    def forward(self, img):
        img = self.conv(img)
        img = img.view(img.size(0), -1)
        out = self.fc(img)
        # out = self.softmax(out)
        
        return out


device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

net = LeNet()
net = net.to(device)

mean = 0.1307
std = 0.3801

# 对图像变换
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((mean,), (std,))
]
)

# 训练数据集, 测试数据集
train_dataset = datasets.MNIST('../datasets/MNIST', train=True, transform=transform, download=True) # len 60000
test_dataset = datasets.MNIST('../datasets/MNIST', train=False, transform=transform, download=True) # len 10000

# 数据迭代器
train_dataloader = DataLoader(train_dataset, batch_size=64, shuffle=True)  # len 938
test_dataloader = DataLoader(test_dataset, batch_size=64, shuffle=True) # len 157

lr = 1e-3
epochs = 20
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
criterion = nn.CrossEntropyLoss()
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', factor=0.5, verbose=True, patience=5, min_lr=0.0000001)
# 训练模型
train_loss = []
train_acc = []
val_loss = []
val_acc = []

for epoch in tqdm(range(epochs)):
    train_losses = 0
    train_acces = 0
    val_losses = 0
    val_acces = 0
    
    for x, y in train_dataloader:
        x, y = x.to(device), y.to(device)
        output = net(x)
        # 计算loss
        loss = criterion(output, y)
        # 计算预测值
        _, pred = torch.max(output, axis=1)
        # 计算acc
        acc = torch.sum(y == pred) / output.shape[0]

        # 反向传播
        # 梯度清零
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        train_losses += loss.item()
        train_acces += acc.item()

    train_loss.append(train_losses / len(train_dataloader))
    train_acc.append(train_acces / len(train_dataloader))

    # 模型评估
    net.eval()
    with torch.no_grad():
        for x, y in test_dataloader:
            x, y = x.to(device), y.to(device)
            output = net(x)
            loss = criterion(output, y)
            scheduler.step(loss)
            _, pred = torch.max(output, axis=1)
            acc = torch.sum(y == pred) / output.shape[0]

            val_losses += loss.item()
            val_acces += acc.item()
        
        val_loss.append(val_losses / len(test_dataloader))
        val_acc.append(val_acces / len(test_dataloader))

    print(f"epoch:{epoch+1}  train_loss:{train_losses / len(train_dataloader):.4f}, train_acc:{train_acces / len(train_dataloader):.4f}, val_loss:{val_losses / len(test_dataloader):.4f}, val_acc:{val_acces / len(test_dataloader)}")

plt.plot(train_loss, color='green', label='train loss')
plt.plot(val_loss, color='blue', label='val loss')
plt.legend()
plt.xlabel("epoch")
plt.ylabel("loss")
plt.show()


plt.plot(train_acc, color='green', label='train acc')
plt.plot(val_acc, color='blue', label='val acc')
plt.legend()
plt.xlabel("epoch")
plt.ylabel("acc")
plt.show()

PATH = './deepfool_mnist_lenet.pth'
torch.save(net, PATH)
 10%|█         | 2/20 [00:25<03:37, 12.08s/it]epoch:2  train_loss:0.0650, train_acc:0.9804, val_loss:0.0563, val_acc:0.9819864649681529
 15%|█▌        | 3/20 [00:37<03:23, 12.00s/it]epoch:3  train_loss:0.0642, train_acc:0.9808, val_loss:0.0553, val_acc:0.9821855095541401
 20%|██        | 4/20 [00:45<02:47, 10.47s/it]epoch:4  train_loss:0.0634, train_acc:0.9810, val_loss:0.0546, val_acc:0.9823845541401274
 25%|██▌       | 5/20 [00:53<02:24,  9.63s/it]epoch:5  train_loss:0.0627, train_acc:0.9812, val_loss:0.0543, val_acc:0.9823845541401274
 30%|███       | 6/20 [01:01<02:06,  9.06s/it]epoch:6  train_loss:0.0621, train_acc:0.9814, val_loss:0.0535, val_acc:0.9827826433121019
 35%|███▌      | 7/20 [01:09<01:53,  8.72s/it]epoch:7  train_loss:0.0616, train_acc:0.9815, val_loss:0.0547, val_acc:0.9822850318471338
 40%|████      | 8/20 [01:17<01:41,  8.48s/it]epoch:8  train_loss:0.0611, train_acc:0.9817, val_loss:0.0530, val_acc:0.9831807324840764
 45%|████▌     | 9/20 [01:25<01:32,  8.42s/it]epoch:9  train_loss:0.0606, train_acc:0.9819, val_loss:0.0525, val_acc:0.9833797770700637
 50%|█████     | 10/20 [01:34<01:23,  8.31s/it]epoch:10  train_loss:0.0603, train_acc:0.9819, val_loss:0.0522, val_acc:0.9834792993630573
 55%|█████▌    | 11/20 [01:42<01:15,  8.40s/it]epoch:11  train_loss:0.0600, train_acc:0.9821, val_loss:0.0525, val_acc:0.98328025477707
 60%|██████    | 12/20 [01:52<01:09,  8.69s/it]epoch:12  train_loss:0.0597, train_acc:0.9822, val_loss:0.0517, val_acc:0.9835788216560509
 65%|██████▌   | 13/20 [02:01<01:03,  9.05s/it]epoch:13  train_loss:0.0595, train_acc:0.9823, val_loss:0.0515, val_acc:0.9836783439490446
 70%|███████   | 14/20 [02:11<00:55,  9.21s/it]epoch:14  train_loss:0.0592, train_acc:0.9824, val_loss:0.0514, val_acc:0.9835788216560509
 75%|███████▌  | 15/20 [02:20<00:46,  9.23s/it]epoch:15  train_loss:0.0590, train_acc:0.9824, val_loss:0.0512, val_acc:0.98328025477707
 80%|████████  | 16/20 [02:30<00:37,  9.32s/it]epoch:16  train_loss:0.0589, train_acc:0.9824, val_loss:0.0517, val_acc:0.9828821656050956
 85%|████████▌ | 17/20 [02:39<00:27,  9.15s/it]epoch:17  train_loss:0.0586, train_acc:0.9825, val_loss:0.0515, val_acc:0.9828821656050956
 90%|█████████ | 18/20 [02:47<00:18,  9.02s/it]epoch:18  train_loss:0.0585, train_acc:0.9825, val_loss:0.0509, val_acc:0.9831807324840764
 95%|█████████▌| 19/20 [02:56<00:08,  8.91s/it]epoch:19  train_loss:0.0583, train_acc:0.9826, val_loss:0.0509, val_acc:0.9831807324840764
100%|██████████| 20/20 [03:06<00:00,  9.33s/it]epoch:20  train_loss:0.0582, train_acc:0.9826, val_loss:0.0521, val_acc:0.9826831210191083

设置deepfool攻击的相关参数

test_dataloader = DataLoader(test_dataset, batch_size=1, shuffle=True) 
max_iter = 10
overshoot = 0.2
def DeepFool(image, label, net, device, num_classes=10, max_iter=50, overshoot=0.02):
    # 源代码中这里输入的image为H*W*3,而我这里为B*H*W*C

    image = image.to(device)
    
    # 源代码这里增维了一次, 我这里有batchsize所以不需要进行增维
    # f_image为经过模型的对各个类别的预测
    # f_image = net.forward(Variable(image[None, :, :, :], requires_grad=True)).data.cpu().numpy().flatten()
    f_image = net(image).data.cpu().numpy().flatten()  # shape:[1, 10] -- [10]


    # argsort(排序,返回在原数据中的索引，从小到大排,使用[::-1]变为了从大到小)
    I = (np.array(f_image)).flatten().argsort()[::-1]

    I = I[0:num_classes]
    # 模型实际预测的标签,我这里改为该数据的真实标签
    # label = I[0]

    # 获取输入图像的形状
    # 源代码输入image是H*W*C,我这里需要降维
    # input_shape = image.cpu().numpy().shape
    input_shape = image.squeeze(dim=0).cpu().numpy().shape
    pert_image = copy.deepcopy(image)

    w = np.zeros(input_shape)  # shape[1, 28, 28]
    r_tot = np.zeros(input_shape) # shape[1, 28, 28]
    
    loop_i = 0
    # 源代码这里又增加一个维度，我只需要直接深拷贝原始图像即可
    # x = Variable(pert_image[None, :], requires_grad=True)
    x = torch.Tensor(pert_image)
    x.requires_grad = True

    fs = net(x)  # fs shape: [1, 10]
    # fs这里的shape是[1,10],所以这里使用fs[0, I[k]],也可以把fs降维成[10]
    # 这是把预测的概率值从大到小放到fs_list中了
    fs_list = [fs[0, I[k]] for k in range(10)]

    # k_i表示添加扰动以后预测的类别,这里对k_i进行初始化
    k_i = label

    while k_i == label and loop_i < max_iter:
        # pert用于存储最小的扰动
        pert = np.inf
        # 计算该预测标签在输入数据x处的梯度
        fs[0, I[0]].backward(retain_graph=True)
        grad_orig = x.grad.data.cpu().numpy().copy()

        for k in range(1, 10):
            # 将模型中所有参数的梯度清零
            zero_gradients(x)
            # x.grad.zero_()

            # 计算第k个标签在输入数据x处的梯度
            fs[0, I[k]].backward(retain_graph=True)
            cur_grad = x.grad.data.cpu().numpy().copy()

            # 计算第k个类别和应预测类别在x梯度的差异,也是扰动应该添加的方向
            w_k = cur_grad - grad_orig
            f_k = (fs[0, I[k]] - fs[0, I[0]]).data.cpu().numpy()

            # 计算了梯度向量w_k的L2范数,pert_k越小，扰动越小，攻击越有效
            pert_k = abs(f_k) / np.linalg.norm(w_k.flatten())

            # 选择最小扰动进行保存
            if pert_k < pert:
                # 需要移动的距离
                pert = pert_k
                # 扰动方向
                w = w_k
        
        r_i = (pert + 1e-4) * w / np.linalg.norm(w)
        # 累加到总扰动上
        r_tot = np.float32(r_tot + r_i)

        pert_image = image + (1 + overshoot) * torch.from_numpy(r_tot).cuda()

        # x = Variable(pert_image, requires_grad=True)
        x = torch.Tensor(pert_image)
        x.requires_grad = True

        fs = net(x)
        # k_i表示预测标签
        k_i = np.argmax(fs.data.cpu().numpy().flatten())

        loop_i += 1
        
    # 放大扰动
    r_tot = (1+overshoot) * r_tot

    return r_tot, k_i, pert_image

生成对抗样本，并进行预测

examples = []
correct = 0

# 产生对抗样本并进行预测类别
for image, label in test_dataloader:
    
    r_t, label_pret, pert_image = DeepFool(image, label, net, device)

    # output = net(pert_image)
    # label_false = torch.argmax(output, dim=1)
    if label == label_pret:
        correct += 1
    else:
        num = random.randint(0, 10)
        if num % 5 == 0 and len(examples) < 10:
            examples.append((pert_image.squeeze().detach().cpu().numpy(), label_pret, image.squeeze().detach().cpu().numpy(), label.cpu().numpy()[0]))
        pass

print(f"Test Accuracy: {correct / len(test_dataloader):.4f}")

可视化

index = 0
plt.figure(figsize=(20, 12))

for i in range(len(examples)):
    index += 1
    pert_image, pert_label, true_image, true_label = examples[i]

    plt.subplot(len(examples), 2, index)
    plt.ylabel("pert_image")
    plt.title("{} --> {}".format(true_label, pert_label))
    plt.imshow(pert_image)

    index += 1
    plt.subplot(len(examples), 2, index)
    plt.ylabel("ori_image")
    plt.title("{} --> {}".format(true_label, true_label))
    plt.imshow(true_image)

plt.tight_layout()
plt.subplots_adjust()

参考文献

DeepFool/Python/deepfool.py at 575f3d847ee65d78c0e3b0306657e3e6d575ba7b · LTS4/DeepFool (github.com)

对抗样本生成系列：FGSM和DeepFool | 小生很忙 (chaoge123456.github.io)

AI安全之对抗样本入门: 5.5 DeepFool算法(deep neural networks,deep fool) - AI牛丝 (ai2news.com)

pytorch实战（二） 在MNIST数据集复现FGSM、DeepFool攻击 | Haoran’s blog (as837430732.github.io)

干货 | 攻击AI模型之DeepFool算法-腾讯云开发者社区-腾讯云 (tencent.com)